1000桶水，其中一桶有毒，猪喝毒水后会在15分钟内死去，想用一个小时找到这桶毒水，至少需要几头猪？-苗华栋

这道题看起来像是一道算法题，本质上却是披着猪皮的信息论 问题。解答这道题并不是我的目的，我的目的是用信息论的思维来思考，达到触类旁通，一通百通。

用信息论去思考的另一个好处就是，信息论给了这类问题的一个边界，让我们在边界范围内思考问题。很难想象，70多年前的香农已经用严格的理论证明为这类问题设定了一个极限，任何想逾越这个极限去解决问题的人最后都会被证明是徒劳的。

这也是理论武装头脑的好处，当别人还在尝试是否有更优的解法时，你可以直接给出最优答案，用信息论降维打击。即使我可能暂时无法想出具体的方案，但我知道这类问题的一个理论极限在哪里，没有必要为超越极限做无用功。

所以，在解题之前我觉得有必要补充一下理论知识，让我们了解一下信息论中“信息熵 ”。

信息熵

1. 热力学中的熵

熵的概念最早起源于物理学，用于度量一个热力学系统的无序程度，也就是系统混乱程序。

熵增定律 指出：

在一个孤立系统里，如果没有外力做功，其总混乱度（熵）会不断增大

熵增定律让我们知道，如果将一杯热水和一杯凉水倒在一起，并且不对水杯中的水做功，这杯水的冷热分子最终一定呈最混乱的分布，也就是最终整体温度均匀分布，绝对不会出现冷热水分层的现象。

如果把宇宙当成一个孤立系统，那么宇宙一定是从有序变为无序混乱的状态，当宇宙的熵达到最大值时，宇宙中的其他有效能量已经全数转化为热能，所有物质温度达到热平衡。这种状态称为热寂。这样的宇宙中再也没有任何可以维持运动或是生命的能量存在。

2. 信息论中的熵

在信息论中，熵的概念和热力学中是类似的，描述的是“信息的不确定程度 ”。

热力学熵：系统的混乱程度
信息熵：信息的不确定性的度量

所以信息中的不确定性类似于热力学中系统的混乱程度。

所以也就是说，信息的不确定程度越大，信息熵也就越大。那什么样的信息不确定程度大呢？

比如抛一枚硬币，如果我来猜正反的话，那么我基本只能靠瞎蒙，因为不确定程度很大，正反的概率都是0.5。对于抛一次硬币猜正反这类事件来说，它的不确定程度很大，信息熵也很大。

如果中国男足和巴西男足比赛，让我来猜胜负，那么我几乎可以断言，巴西队一定会赢。也就是巴西队和中国队胜负这个事件的不确定程度很小，信息熵也就很小。

如果比赛后巴西队真的赢了，那么这条信息的信息量几乎为零，因为这条信息几乎没有降低信息的不确定度。

上面提到了信息熵、信息、信息量 ，它们之间的比较如下：

信息熵 是一个绝对值，用来衡量信息不确定程度的绝对大小。
凡是在一种情况下能减少不确定性的任何事物都叫信息， 否则叫作废话**。** 比如经常会碰到有人絮絮叨叨，不知所云，说了好久不知道要表达什么。从信息论的角度来看，这些话就不包含信息。
信息量 是一个相对值，表示的是在某个具体事件发生以后所带来的的信息。显然，事件发生的概率越低，当事件发生了以后带来的信息越大，说明信息量越大。比如福彩35选7，如果有人直接告诉你这7个数字，开奖了以后竟然是一样的，那么这条信息的信息量就超级大。又比如某报刊登了男明星A出轨的消息，因为我们已经知道男明星A本身就很渣，出轨也在情理之中，所以这则消息的信息量就很低。

上面都只是定性的分析，香农把随机变量 X 的熵值 Η定义如下，其值域为{x 1, …, xn}

$mathrm{H} X=-sum x{i}log {b}{mathrm {P}}x{i}}$

b是对数所使用的底。当 b = 2，熵的单位是bit 。

P为 X 的概率质量函数（probability mass function），我们可以理解为事件xi 发生的概率。

公式看起来可怕，其实非常简单。

让我们用抛硬币来举例，“抛一次硬币是正面”这个随机变量X的信息熵 为

$mathrm{H} X=-frac{1}{2}log _{2}frac{1}{2} + frac{1}{2}log {2}frac{1}{2} = -log{2}frac{1}{2}=1$

也就是抛一次硬币是正面这个事件的信息熵只需要1 bit，也就是只需要用1位的二进制数就可以表示这个信息大小。

题目的简化版本

在我们学习了信息熵的知识以后，让我们再来看题目。原题其实略微复杂一些，先将题目简化一下。

1000桶水，其中一桶有毒，猪喝毒水后会在15分钟内死去，想用15分钟内找到这桶毒水，至少需要几头猪？

上面这道题其实也是当年google的一道面试题，只不过面试题中的小白鼠在这里被替换成了猪。原题是多次试验问题，简化后的版本是单次试验，更容易看到这道题的本质。于是我们利用上面介绍的信息熵的知识来求解一下。

首先，”1000桶水其中有一桶有毒 “这个随机变量X的信息熵 为

$mathrm{H} X=-log _{2}frac{1}{1000} =9.966$

1只猪喝水以后的要么活着，要么死去，一共有两种状态，所以”1只猪喝完水以后的状态“这个随机变量Y的信息熵为

$mathrm{H} Z=-frac{1}{2}log _{2}frac{1}{2} + frac{1}{2}log {2}frac{1}{2} = -log{2}frac{1}{2}=1$

n只猪喝完水会有 $2^n$ 种状态，即"n只猪喝完水以后的状态"这个随机变量Y的信息熵为

$mathrm{H} Y=-sum _{2n}{frac{1}{2^n}}{log _{2}{frac{1}{2^n}}}=-log _{2}{frac{1}{2^n}}=n$

所以，按照题目要求，如果至少需要n头猪能够找到这桶毒水，那么随机变量Y的信息熵必须要大于随机变量X的信息熵，也就是

H(Y) >= H(X) ，也就是 n >= 9.966，即 n = 10

当我们用信息熵算出来了n的最小值以后，我们就可以坚信，理论上n=10一定是最优解，任何想方设法想找到小于10的值都是徒劳的。

其实，上面的信息熵计算的简化版本可以写成如下更好理解的形式

$2^n ge 1000$

同样可以解得 n = 10 ，虽然形式简单，但我们一定要记住它背后的原理是信息熵。

至于到底采用什么方案，这涉及到术的层面，即使我们暂时想不到，我们也会有努力的方向，并且知道努力的边界在哪里，不会做类似寻找永动机的事情。

下面我们来看下图具体的方案

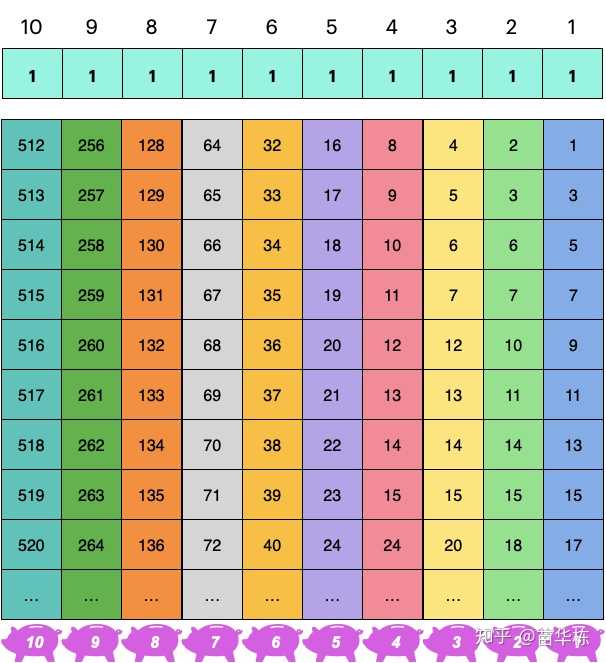
我们将1000桶水按照2进制编码，如上图第一行，需要10位二进制数。于是有

第1桶水对应上图最右侧位置1的数字是1，其它数字都是0，也就是00000 00001b，其中b代表二进制数。
第10桶水对应上图位置4和位置2的数字是1，其它数字都是0，也就是 00000 01010b。
同理，任意一桶水，都可以对应上面唯一的一个二进制数。

于是，我按照如下方案让猪进行喝水，如上图所示：

1号猪喝位置1的数字是1的水，也就是1、3、5、7、9 …
2号猪喝位置2的数字是1的水，也就是2、3、6、7、10 …
…
6号猪喝位置6的数字是1的水，也就是32、33、34、35、36 …
…

如果15分钟后1，3，5号猪被毒死，那么对应的二进制编码就是00000 10101b，也就是21号水桶有毒。更一般的，猪死的任何一种排列方式都对应了二进制的唯一编码。

这里为什么采用二进制的编码方式？

首先，我们要理解为什么计算机内部运算都采用二进制的方式，这是因为开关电路在计算机中实现起来非常简单，而开关两种状态正好对应了二进制的0和1。老式的计算机都是用继电器的开关实现的，而现代计算机也是利用逻辑电路的通断实现高低电压来表示0和1。所以计算机内部的运算其实都是将其转化为二进制再进行运算的。

而猪的生死正好对应了计算机中的开关电路，所以我们这里采用二进制进行编码。

而原题目多次试验的情况就不能采用二进制编码了。

原题目

1000桶水，其中一桶有毒，猪喝毒水后会在15分钟内死去，想用一个小时找到这桶毒水，至少需要几头猪？

有了前面简化的版本的理解，我们容易得知

”1000桶水其中有一桶有毒 “这个随机变量X的信息熵 为

$mathrm{H} X=-log _{2}frac{1}{1000} =9.966$

而对于猪的状态就不太一样了，我们可以想象一下，一只猪在一个小时内会有几种状态？

在第0分钟的时候喝了一桶水以后，第15分钟死去。
第15分钟依然活着，喝了一桶水以后，第30分钟死去。
第30分钟依然活着，喝了一桶水以后，第45分钟死去。
第45分钟依然活着，喝了一桶水以后，第60分钟死去。
第45分钟依然活着，喝了一桶水以后，第60分钟依然活着。

可见，1只猪1个小时以后会有5种状态，所以”1只猪1个小时后的状态“这个随机变量Z的信息熵为

$mathrm{H} Z=- 5 times frac{1}{5}log {2}frac{1}{5} = log{2}5=2.3219$

n只猪1个小时后会有 $5^n$ 种状态，即"n只猪1个小时以后的状态"这个随机变量Y的信息熵为

$mathrm{H} Y=-sum _{5n}{frac{1}{5^n}}{log _{2}{frac{1}{5^n}}}=-log {2}{frac{1}{5^n}}=n log{2}{5}=2.3219n$

所以，按照题目要求，如果至少需要n头猪能够找到这桶毒水，那么随机变量Y的信息熵必须要大于随机变量X的信息熵，也就是

H(Y) >= H(X) ，也就是 n >= 9.966 / 2.3219 = 4.292，即 n = 5

事实上，对于 n = 5来说，不仅可以检测1000桶水，甚至检测3000桶水都是没有问题的。有兴趣的童鞋可以试着计算一下 。

到此，香农给了我们一个理论极限，但是具体的方案还是需要我们自己进行构造。得出n=5是依靠我们的理论功底，而得出具体的方案就是我们的工程水平了。

根据前面简化版本的二进制编码方式的思路，我们是不是可以利用猪的5种状态构造一个5进制编码方式呢？如下图所示。

首先，将1000桶水按照5进制编码的方式排列，如上图所示，需要5位5进制数。

然后按照如下方案让猪进行喝水，如上图所示：

1号猪第0分钟喝位置1的数字是1的水，如图所示，也就是1、6、11、16、21…
如果第15分钟活着，喝位置1的数字是2的水，如图所示，也就是2、7、12、17、22…
如果第30分钟活着，喝位置1的数字是3的水，如图所示，也就是3、8、13、18、23…
如果第45分钟活着，喝位置1的数字是4的水，如图所示，也就是4、9、14、19、24…
类似的，2号猪喝位置2的水…

上面，猪的编号代表5进制编码数字所在的位数，1号猪代表最末位，5号猪代表最高位。而第几分钟死代表当前位数的权重，15分钟死表示权重是1，30分钟死表示权重是2，… ，60分钟死表示权重是4，60分钟依然活着表示权重是0。

如果1号猪第30分钟死了，2号猪第15分钟死了，3号猪第45分钟死了，4，5号都活到了最后。则毒水对应的5进制编码是

$0 times 5^4 + 0 times 5^3 + 3 times 5^2 + 1 times 5^1 + 2times5^0 = 82$

也就是第82桶水有毒。

到此，这个问题从理论和工程上都给出了答案。信息熵让我们明确了工程上努力的方向并明确了那条不可逾越的鸿沟。

熵的拓展

前面提到了热力学中的“熵增定律”，其实在社会中“熵”也有重要的意义。

对于国家来说，如果闭关锁国，相当于一个孤立系统，就好比鸦片战争前的清政府，不与外界进行交流，也不进行贸易，也就相当于没有能量的交换，最终的结果必定是“熵增”，即越来越混乱，越来越没有效率。

所以必须保持对外开放的政策，与外界环境不间断的交换。比如：与世界各国进行贸易往来，招商引资，引进竞争，这些都是“负熵”的表现。

对于企业也是同理，必须引进“负熵”，比如现代化的管理方式，先进的技术等等。否则，企业内部不了解外部经济环境变化，也不了解终端用户，只能是最终能量耗尽而亡。

最后，希望本篇回答让你不仅了解了题目本身，更能知道信息论在解决类似问题时给出的指导意义，让我们具备自顶而下的思考方式，首先直击问题本质，将现实问题抽象成数学或者其他已知问题，然后用理论给出答案的边界，也明确的努力的方向和极限。接下来在工程上，保证在理论边界内去尝试，而不是一味地试图超越理论极限，做无用功。

而常人的做法往往是先尝试一种方案，发现应该还有优化空间，于是逐步优化，但是不知道努力的方向和边界。

所以往往要么在努力的过程中离边界值还有很大距离的时候就放弃了，要么就是试图突破边界而做无用功，要么努力了一大顿最后才发现极限的优化提升空间也只有2%，不得不更换方案。

这可能也是高手与常人的区别，希望本文能让大家了解这种自顶向下的思考方式。

2020-6-10号更新

看到评论中有很多对答案有疑问的，所以补充一下答疑，不一一回复了，谢谢。

1. 有的评论说，一只猪就够，每隔两秒钟喝一次。

请参见题目详情限制条件1

“1.一滴毒水足以导致一头猪的死亡。死亡时间为15分钟内不确定的某个时间点。”

请仔细审题，不是恰好15分钟，而是最长15分钟。猪每隔两秒喝一次即使死了也是无法区分哪桶水有毒的。

仔细审题很重要啊！

2. 为什么题目中在计算猪的信息熵时采用了等概率？

很抱歉，这个我在解释的过程中忽略了。

首先要明确的是，猪在喝毒水的时候生和死的概率确实不一定是等概率的，这个是对的。

比如原题中，对于5号猪来说，因为它喝的水位于5进制的最高位上，所以它活的概率是 $frac{624}{1000} = 0.624$ 。

既然不是等概率，那正文中为什么采用等概率的方式呢？这是因为在计算信息熵的时候，我们考虑的是n只猪所能表达的最大信息熵。

数学上可以证明，当随机事件等概率发生的时候，信息熵是最大的 。

题目要求最少n只猪，意思就是在最差情况下用n只猪也能找到毒水。而最差的情况就是每只猪生死的概率是相等的。

所以我们用等概率的方式求出最大信息熵时最小的n，当n再小，最差情况下已经无法测出1000桶水了。

如果你觉得对你有帮助，请帮忙点赞，谢谢。

评论区

GrossteAnmassung: 看完这个回答我只想说一句话——教练，我想学信息论！ 👍🏽1344 💭N/A IP 🕐2020-06-10 04:02:53

│ └── 贤者时间: 猪说：下辈子不做猪了 👍🏽241 💭N/A IP 🕐2020-06-10 14:44:08
│ │ └── 迎风骑猪向前冲: 猪到底到什么罪了，非得死？ 👍🏽0 💭N/A IP 🕐2020-06-19 16:17:47
│ │ └── 王晰: / #！…… 👍🏽1 💭N/A IP 🕐2020-06-26 09:26:02
│ └── 喝着牛奶的nobody: 当兴趣学可以，要考试是真的头痛[捂脸] 👍🏽81 💭N/A IP 🕐2020-06-10 15:19:52
│ │ └── 生民何计乐樵苏: 还行，我们信息论与编码是专业必选课，最后是开卷[捂脸] 👍🏽9 💭N/A IP 🕐2020-06-10 20:17:34
│ │ └── Halfapear: 点了 👍🏽0 💭N/A IP 🕐2024-12-10 22:09:04
│ └── 狗蛋儿: 教练，我想学养猪[飙泪笑] 👍🏽5 💭N/A IP 🕐2020-06-10 20:50:30
│ └── 蹭风手: 上次作弊被抓跳楼的好像就学的这玩意[为难] 👍🏽21 💭N/A IP 🕐2020-06-10 20:51:00
│ └── 李苌春: 不，你不想。通信专业老学长直呼内行。 👍🏽3 💭N/A IP 🕐2020-06-11 16:50:10
│ └── David: 通信的学渣上学期期末差点栽在概率与统计部分的信息论章节了[捂脸] 👍🏽2 💭N/A IP 🕐2020-06-11 17:30:44
│ │ └── 种桃道士: 概率论只学前八章[吃瓜] 👍🏽0 💭N/A IP 🕐2021-07-26 15:42:53
│ └── 云卷云舒ily: 上学期期末差点没把我整崩溃 👍🏽0 💭N/A IP 🕐2020-06-11 20:48:24
│ └── 城寨归来者: 好好看看底下业内人士的嚎哭吧，通信系统才是大学里面的蜀山修仙派。反正我是直接自行除籍下山摆摊算命去了。 👍🏽3 💭N/A IP 🕐2020-06-12 06:24:40
│ └── 知乎用户vA5V3g: 我已经默默打开b站搜信息论 👍🏽0 💭N/A IP 🕐2020-06-22 23:39:48
│ └── 烫就冷一会再吃: 通信原理就有讲 👍🏽0 💭N/A IP 🕐2020-06-28 01:57:34
│ └── 王书庆: 我看完也想学呢，觉得挺有意思的。 👍🏽0 💭N/A IP 🕐2020-08-27 17:23:28
│ └── Andy: 订吴军的信息论50讲 👍🏽1 💭N/A IP 🕐2020-08-30 17:50:56
│ └── Nihil: 刚学完信息论（入门级[捂脸] 👍🏽0 💭N/A IP 🕐2020-09-23 17:39:45
│ └── super: 俺也一样 👍🏽0 💭N/A IP 🕐2021-06-02 18:12:33
│ └── 知乎用户rmr9Rs: 用一只猪，一分钟喝23桶水（45分钟内喝完），死时往前推15分钟即可算出那一桶，期间保证喂水时胃中浓度。所以。。一只即可。 👍🏽0 💭N/A IP 🕐2021-07-25 10:08:10
│ │ └── 无名: 猪撑死了怎么办[捂脸] 👍🏽0 💭N/A IP 🕐2023-02-20 05:33:34
│ └── 电电牛: 大学理工科基础课程概率论就有，讲道理不是很难理解 👍🏽0 💭N/A IP 🕐2021-10-21 14:36:05
│ └── momo: 西电通信狗路过表示你替我呗[捂脸] 👍🏽0 💭N/A IP 🕐2021-10-26 16:06:58
│ └── 爱滚的刺猬: 大一公共课貌似学过一点，没想到可以这么难[流泪] 👍🏽0 💭N/A IP 🕐2022-01-17 12:22:04

风笛: 每个字都认识[大哭] 👍🏽1602 💭N/A IP 🕐2020-06-10 09:03:01

│ └── misaka: 就是看不懂[惊喜] 👍🏽118 💭N/A IP 🕐2020-06-10 13:40:56
│ └── 王若谷: 看一下李永乐老师有期视频讲的，比这个好懂，当然这个也很棒，但是水桶如何编码哪里没讲清楚。 👍🏽46 💭N/A IP 🕐2020-06-11 17:52:00
│ └── 王若谷: https://b23.tv/rP4kyw 👍🏽5 💭N/A IP 🕐2020-06-11 17:55:48
│ │ └── 赵小鱼: 感觉五人一组做核酸检测也是这个道理 👍🏽1 💭N/A IP 🕐2020-09-26 11:56:33
│ │ └── May: 这个方法有漏洞 👍🏽0 💭N/A IP 🕐2020-09-26 13:49:03
│ │ │ └── 赵小鱼: 为什么呢？ 👍🏽0 💭N/A IP 🕐2020-09-27 01:14:21
│ │ │ └── May: 因为核酸检测的方式好像是聚集式的如果聚集时测试的抽检结果是没有问题的那聚集之后呢而且总感觉这个检测测的是不是别的 👍🏽0 💭N/A IP 🕐2020-10-04 18:58:40
│ │ └── 王若谷: 有相似的地方，但核心不同，这个涉及到十进制二进制的转换，思想太精妙了 👍🏽1 💭N/A IP 🕐2021-05-27 19:26:12
│ └── 鸿鹄何惧鸿沟: 那你算厉害的熵我就不认识，能打出来还是手写的 👍🏽5 💭N/A IP 🕐2020-06-12 07:25:52
│ │ └── 念念不南国: 妹的，害的我手打了一遍才知道它到底读什么 👍🏽0 💭N/A IP 🕐2021-08-04 23:06:16
│ └── 我亦飘零久: 那个公式里的侧着写的M不认识[捂脸] 👍🏽0 💭N/A IP 🕐2020-06-12 08:21:47
│ │ └── Rain-TNS: 求和符号∑（sigma）啊 👍🏽1 💭N/A IP 🕐2020-06-12 09:46:36
│ └── sunky: 哈哈哈哈哈哈哈哈哈哈哈哈哈 👍🏽0 💭N/A IP 🕐2020-06-12 14:38:45
│ └── 神尾观铃: 解释的比较绕，本质其实还算好理解，1小时对应5种可能，剩下的5的次方数就是验证的数量。5的4次方只能验证625桶，不够1000，5次方是3215，可以验证3125桶水。结论需要5头猪。这个算法如果不是用的多，确实很难想到，至于最后的展开，其实就是从1维到5维的一个变形而已。 👍🏽8 💭N/A IP 🕐2020-06-12 16:39:58
│ └── 神尾观铃: 简单的说，1小时有5种结果，对应基数就是5，几头猪，就是5的几次方，4头猪就是5的4次方625次，不够1千，5头猪就是5的5次方，3125，大于一千，所以5头猪。至于最后查出来是哪一桶水，这个变换我倒是第一次看到成体系的解释，以前都是想过但不知道怎么解释出来，就是那种考试直接写答案但不知道怎么描述过程的感觉。 👍🏽9 💭N/A IP 🕐2020-06-12 16:43:56
│ └── 云和月: 那个躺倒的大号M我就不认识 👍🏽0 💭N/A IP 🕐2020-06-13 00:01:11
│ └── 啦啦啦: 这个名字，是刀客塔吗[好奇] 👍🏽0 💭N/A IP 🕐2020-06-14 15:19:59
│ └── 加贝: 我连字都有不认识的是在下输了[微笑] 👍🏽0 💭N/A IP 🕐2020-10-20 10:28:45
│ └── 柳飞扬: 买书来看 👍🏽0 💭N/A IP 🕐2021-02-22 10:36:02
│ └── 噗啦噗啦豆: 呃，那个字念啥？di? 👍🏽0 💭N/A IP 🕐2021-05-28 15:30:24
│ │ └── YoRHa9Type S: 熵（shang）一声，高中化学和物理都会学到，表混乱程度 👍🏽0 💭N/A IP 🕐2021-07-22 01:28:08
│ └── Ztdd: 什么都没说也什么都说了[赞同] 👍🏽0 💭N/A IP 🕐2021-08-06 19:35:08
│ └── 江湖人称: 连有的字我都不认识咋整[口罩] 👍🏽0 💭N/A IP 🕐2021-10-21 13:18:35

GrossteAnmassung: 没想到今晚刷到你这篇回答，真是有幸，对我有一种打开了新世界大门的感觉[害羞] 👍🏽386 💭N/A IP 🕐2020-06-10 05:05:41

│ └── 相信自己: 我觉得吧，如果说你用肉眼和鼻子分不出来，那个毒一定是无色无味的，肯定也没有腐蚀性，那完全可以把1000桶水全部混在一起，我觉得它的毒性就已经削弱到不足以致死。 👍🏽8 💭N/A IP 🕐2020-06-11 21:11:22
│ │ └── 荒芜之年: emmmm，你得看浓度啊，有些剧毒物质一桶浓度很高分散到一千你被毒死的可能性还是很大的 👍🏽18 💭N/A IP 🕐2020-06-11 21:41:06
│ │ └── 一块黑夜: 你没读完整题目就过来答题，考试大忌啊伙计 👍🏽41 💭N/A IP 🕐2020-06-12 03:01:00
│ │ │ └── 小米: 好家伙期末考试之前要是看见了你这句话我语文肯定能上120 👍🏽3 💭N/A IP 🕐2020-07-29 23:48:59
│ │ │ └── 小米: 好家伙期末考试之前要是看见了你这句话我语文肯定能上120 👍🏽3 💭N/A IP 🕐2020-07-29 23:48:59
│ │ └── 勃勃生机: 氢氰酸表示不服 👍🏽6 💭N/A IP 🕐2020-06-16 21:58:03
│ │ └── hyyy: 这是个数学问题，不是化学问题，要抓重点，ok? 👍🏽9 💭N/A IP 🕐2020-06-22 14:05:15
│ │ └── 耶律阿保呀: 没必要这样，不然你可以蒸馏一桶浓缩成一滴也未尝不可 👍🏽0 💭N/A IP 🕐2021-07-31 02:23:50
│ │ └── enjou: 这是个理论问题关键在于解题思路所有表现性的文字都只是用于表达逻辑的人活着要活得明白活得透彻内在啊你这看得有点表面了[捂脸] 👍🏽0 💭N/A IP 🕐2021-07-31 16:24:55
│ │ └── 荒芜之年: emmmm，你得看浓度啊，有些剧毒物质一桶浓度很高分散到一千你被毒死的可能性还是很大的 👍🏽18 💭N/A IP 🕐2020-06-11 21:41:06
│ │ └── 一块黑夜: 你没读完整题目就过来答题，考试大忌啊伙计 👍🏽41 💭N/A IP 🕐2020-06-12 03:01:00
│ │ │ └── 小米: 好家伙期末考试之前要是看见了你这句话我语文肯定能上120 👍🏽3 💭N/A IP 🕐2020-07-29 23:48:59
│ │ │ └── 小米: 好家伙期末考试之前要是看见了你这句话我语文肯定能上120 👍🏽3 💭N/A IP 🕐2020-07-29 23:48:59
│ │ └── 勃勃生机: 氢氰酸表示不服 👍🏽6 💭N/A IP 🕐2020-06-16 21:58:03
│ │ └── hyyy: 这是个数学问题，不是化学问题，要抓重点，ok? 👍🏽9 💭N/A IP 🕐2020-06-22 14:05:15
│ │ └── 耶律阿保呀: 没必要这样，不然你可以蒸馏一桶浓缩成一滴也未尝不可 👍🏽0 💭N/A IP 🕐2021-07-31 02:23:50
│ │ └── enjou: 这是个理论问题关键在于解题思路所有表现性的文字都只是用于表达逻辑的人活着要活得明白活得透彻内在啊你这看得有点表面了[捂脸] 👍🏽0 💭N/A IP 🕐2021-07-31 16:24:55
│ └── 不善言谈: 卧槽我什么时候才有有你一根指头优秀 👍🏽0 💭N/A IP 🕐2020-09-25 13:03:24
│ └── 月华: 我有一种被新世界的大门打了一顿不让进去的感觉[捂脸][捂脸] 👍🏽1 💭N/A IP 🕐2021-08-02 12:10:59
│ └── 相信自己: 我觉得吧，如果说你用肉眼和鼻子分不出来，那个毒一定是无色无味的，肯定也没有腐蚀性，那完全可以把1000桶水全部混在一起，我觉得它的毒性就已经削弱到不足以致死。 👍🏽8 💭N/A IP 🕐2020-06-11 21:11:22
│ │ └── 荒芜之年: emmmm，你得看浓度啊，有些剧毒物质一桶浓度很高分散到一千你被毒死的可能性还是很大的 👍🏽18 💭N/A IP 🕐2020-06-11 21:41:06
│ │ └── 一块黑夜: 你没读完整题目就过来答题，考试大忌啊伙计 👍🏽41 💭N/A IP 🕐2020-06-12 03:01:00
│ │ │ └── 小米: 好家伙期末考试之前要是看见了你这句话我语文肯定能上120 👍🏽3 💭N/A IP 🕐2020-07-29 23:48:59
│ │ │ └── 小米: 好家伙期末考试之前要是看见了你这句话我语文肯定能上120 👍🏽3 💭N/A IP 🕐2020-07-29 23:48:59
│ │ └── 勃勃生机: 氢氰酸表示不服 👍🏽6 💭N/A IP 🕐2020-06-16 21:58:03
│ │ └── hyyy: 这是个数学问题，不是化学问题，要抓重点，ok? 👍🏽9 💭N/A IP 🕐2020-06-22 14:05:15
│ │ └── 耶律阿保呀: 没必要这样，不然你可以蒸馏一桶浓缩成一滴也未尝不可 👍🏽0 💭N/A IP 🕐2021-07-31 02:23:50
│ │ └── enjou: 这是个理论问题关键在于解题思路所有表现性的文字都只是用于表达逻辑的人活着要活得明白活得透彻内在啊你这看得有点表面了[捂脸] 👍🏽0 💭N/A IP 🕐2021-07-31 16:24:55
│ │ └── 荒芜之年: emmmm，你得看浓度啊，有些剧毒物质一桶浓度很高分散到一千你被毒死的可能性还是很大的 👍🏽18 💭N/A IP 🕐2020-06-11 21:41:06
│ │ └── 一块黑夜: 你没读完整题目就过来答题，考试大忌啊伙计 👍🏽41 💭N/A IP 🕐2020-06-12 03:01:00
│ │ │ └── 小米: 好家伙期末考试之前要是看见了你这句话我语文肯定能上120 👍🏽3 💭N/A IP 🕐2020-07-29 23:48:59
│ │ │ └── 小米: 好家伙期末考试之前要是看见了你这句话我语文肯定能上120 👍🏽3 💭N/A IP 🕐2020-07-29 23:48:59
│ │ └── 勃勃生机: 氢氰酸表示不服 👍🏽6 💭N/A IP 🕐2020-06-16 21:58:03
│ │ └── hyyy: 这是个数学问题，不是化学问题，要抓重点，ok? 👍🏽9 💭N/A IP 🕐2020-06-22 14:05:15
│ │ └── 耶律阿保呀: 没必要这样，不然你可以蒸馏一桶浓缩成一滴也未尝不可 👍🏽0 💭N/A IP 🕐2021-07-31 02:23:50
│ │ └── enjou: 这是个理论问题关键在于解题思路所有表现性的文字都只是用于表达逻辑的人活着要活得明白活得透彻内在啊你这看得有点表面了[捂脸] 👍🏽0 💭N/A IP 🕐2021-07-31 16:24:55
│ └── 不善言谈: 卧槽我什么时候才有有你一根指头优秀 👍🏽0 💭N/A IP 🕐2020-09-25 13:03:24
│ └── 月华: 我有一种被新世界的大门打了一顿不让进去的感觉[捂脸][捂脸] 👍🏽1 💭N/A IP 🕐2021-08-02 12:10:59

三千: 这才是知乎应有的答案 👍🏽159 💭N/A IP 🕐2020-06-10 11:57:35

小池塘里的啦嘎布: 太强了，学不会[捂脸] 👍🏽113 💭N/A IP 🕐2020-06-10 07:37:11

│ └── 星星点灯: . 👍🏽0 💭N/A IP 🕐2020-06-10 14:12:07
│ └── 江南雪飘: 不要灰心，你能学废的[大笑] 👍🏽0 💭N/A IP 🕐2021-07-25 18:36:29
│ │ └── 小池塘里的啦嘎布: 已经废了[赞同] 👍🏽0 💭N/A IP 🕐2021-07-25 20:27:10
│ │ └── 在禁言与解封之间: 还能更废，比如我[惊喜] 👍🏽0 💭N/A IP 🕐2021-07-26 17:58:21
│ │ └── 咿呀咿呀: 兄弟你这不对啊，首先一千不是开3次方么，再说了能不能很快找出有毒的那桶，得看毒发时间的长短啊 👍🏽0 💭N/A IP 🕐2021-08-05 16:43:03
│ └── 红尘练心: 我算出来是8头，1000开4次方向上取整=6。每次分成6份喂5头猪。5+1+1+1=8 👍🏽2 💭N/A IP 🕐2021-08-03 14:46:04
│ └── 祝思聪: 别人答案写了这么多你是一点没看啊[尴尬]已经给出了最高效的方案，你还要用你朴素又低效的方法 👍🏽0 💭N/A IP 🕐2024-01-24 13:07:59

Lloyd: 不想喝猪喝过的水咋办 👍🏽102 💭N/A IP 🕐2020-06-10 08:07:45

│ └── 搪瓷丝: 你可以倒出来一点给猪喝啊 👍🏽209 💭N/A IP 🕐2020-06-10 12:39:33
│ │ └── 冥溟: 哈哈哈 👍🏽8 💭N/A IP 🕐2020-06-10 14:19:23
│ │ └── 就叫qht啊: 笑死[飙泪笑][飙泪笑] 👍🏽6 💭N/A IP 🕐2020-06-10 15:15:24
│ │ └── 林瑜: 一个敢问一个敢答 👍🏽46 💭N/A IP 🕐2020-06-10 18:38:32
│ │ └── BOKI人: 抛开剂量谈毒性[生气] 👍🏽0 💭N/A IP 🕐2021-10-21 14:35:21
│ └── 时光基: 哈哈哈哈哈哈哈哈 👍🏽0 💭N/A IP 🕐2020-06-10 20:55:29
│ └── 名杨: 多大的桶才能让500头猪都有水喝啊。 👍🏽0 💭N/A IP 🕐2020-06-10 23:11:51
│ │ └── 我是千玺本玺: 一猪10滴，5000滴水也不多 👍🏽0 💭N/A IP 🕐2020-06-11 19:42:29
│ │ └── 蒋啰啰: 10滴毒死一头几百公斤的🐷，那不是水里有毒，那是毒里掺了水吧！希望🐷没事[拜托] 👍🏽14 💭N/A IP 🕐2020-06-11 20:50:24
│ │ └── 我是千玺本玺: 现在流行不看题，硬杠么[捂脸] 👍🏽1 💭N/A IP 🕐2020-06-11 23:38:21
│ │ └── Nagakive: 就硬杠，这世界上也不存在喝了之后正正好好15分钟死的有毒物质啊 👍🏽1 💭N/A IP 🕐2020-06-12 09:11:51
│ │ └── 咸鱼干: 题目说的是15分钟内，到你这就变成15分钟整，你以为是定时炸弹吗[摊手] 👍🏽0 💭N/A IP 🕐2020-09-16 08:59:47
│ └── Sunnix: 嘴对嘴喂他 👍🏽0 💭N/A IP 🕐2020-06-12 16:14:01
│ └── May: 你可以自己去喝 👍🏽1 💭N/A IP 🕐2020-09-26 13:47:24
│ └── 咿呀咿呀: 不是让猪试毒么，你不想喝就不呗[大笑] 👍🏽0 💭N/A IP 🕐2021-08-05 16:44:45
│ └── 用户5997893: 那你先喝再给猪喝 👍🏽0 💭N/A IP 🕐2021-12-29 23:59:07

null: 我以为是讲算法，结果讲的是信息论，太强了 👍🏽76 💭N/A IP 🕐2020-06-10 10:24:57

牛奶咖啡8023: 感觉我的信息论白学了。。。哦，压根就没好好学过[捂脸] 👍🏽62 💭N/A IP 🕐2020-06-10 08:41:48

│ └── 行云流水: 同感，信息论白学了。。 👍🏽4 💭N/A IP 🕐2020-06-11 18:05:44
│ └── 罗洛落: 问题是前不久才刚考过试也感觉打开了新世界的大门 👍🏽7 💭N/A IP 🕐2020-06-11 20:04:09
│ │ └── 行者: 所以，你这是薛定谔的门么？[捂脸][捂脸][捂脸] 👍🏽0 💭N/A IP 🕐2020-10-05 23:37:25
│ │ └── 罗洛落: 没能系统深刻的理解，就会编码了[捂脸] 👍🏽0 💭N/A IP 🕐2020-10-05 23:41:46
│ └── Mason: 信息论基础看到第三页的例子都比这复杂…你肯定是白学了 👍🏽0 💭N/A IP 🕐2022-04-30 08:52:41

邓尚平: 一头猪是1bit，原问题转化为表示1000个数最少需要几位bit，妙啊 👍🏽52 💭N/A IP 🕐2020-06-10 11:42:20

│ └── 四处游荡的风: 我一直觉得这种问题突然转化成编码很奇怪。现在才知道，原来是信息论在牵线搭桥。 👍🏽6 💭N/A IP 🕐2020-06-10 13:49:38
│ │ └── 令狐重阳: 其实用决策树去理解更方便一点 👍🏽1 💭N/A IP 🕐2020-06-12 08:33:14
│ └── neisdx: 本来没看懂，看到你的答案懂了。是不是这样理解，1头猪包含5bit信息，所以用5进制数，5头猪就是5∧5＝3125bit，4头猪是625bit，4头猪信息量不足，5头就满足要求，理论上5头猪最多可以找出3125桶水中的一桶毒水 👍🏽59 💭N/A IP 🕐2020-06-10 15:50:55
│ │ └── 贪梦: 为什么是5bit阿。。 👍🏽0 💭N/A IP 🕐2020-06-10 17:24:14
│ │ │ └── neisdx: 一头猪有5种情况：15分钟死，30分钟死，45分钟死，60分钟死，活。所以是5bit 👍🏽9 💭N/A IP 🕐2020-06-10 17:49:26
│ │ │ └── 尹立岩: [捂脸]60分钟之前，不死不让跑 👍🏽1 💭N/A IP 🕐2020-06-10 19:27:04
│ │ │ └── 陈愚: 不是5bit,只是五种状态而已，想要它是5bit的话，你得会复活法术，猪死了你还能把它复活过来继续做实验，这样的话，每个猪就不是五种状态了，而是16种状态了。 👍🏽6 💭N/A IP 🕐2020-06-17 08:34:24
│ │ │ └── hyyy: 不是5bit，5bit是指2^5=32种情况 👍🏽1 💭N/A IP 🕐2020-06-22 14:10:46
│ │ └── 互联网海贼: 其实不叫5bit，bit就是二进制的一位，五个信息量的一位，应该叫fit[思考] 👍🏽19 💭N/A IP 🕐2020-06-10 21:37:49
│ │ │ └── 水木光华: 妙啊，1进制的话等于没有，2进制为啥叫bit不叫double的dit，三个信息量比如天平就是trit还是tit？4进制和5进制你这样分不清，4的叫夸他kill，qit，5杀当然是喷他kill，pit，怪不得四杀五杀要有区别，带师，我悟了。那么问题来了，six seven怎么分呢？6it 7it？ 👍🏽0 💭N/A IP 🕐2021-07-05 09:53:16
│ │ └── 涅槃: 5^5-1 👍🏽0 💭N/A IP 🕐2020-06-20 16:49:48
│ │ └── 知乎用户ZbKYfs: 做为一个程序猿，直觉是想当做算法来解题，看了这个回答觉得很有意思，但仔细一想，算法上就是遍历了一次啊。。。 👍🏽0 💭N/A IP 🕐2020-06-22 12:05:42
│ │ └── 在家里流浪: 我去，楼主的没看懂，你这个我顿时看懂了~ 👍🏽0 💭N/A IP 🕐2021-06-07 18:13:56
│ │ └── 在家里流浪: 或者说，你这个我假装看懂了。 👍🏽0 💭N/A IP 🕐2021-06-07 18:14:17
│ │ └── 老马: 虽然不懂你说的这个东西，但是题目中按几进制来是取决于猪有几种可能的状态。第一次用二进制是因为以十五分钟一次，猪只有死和活两种状态。第二次，一个小时的时间了，猪有四个时间段可以死，加上活着的这一种情况，一共有五种可能的状态，所以采用五进制，把1.2.3.4.5分别代表一种状态。 👍🏽2 💭N/A IP 🕐2021-07-26 09:35:21
│ └── 转折跳跃: 是5进制 👍🏽0 💭N/A IP 🕐2021-06-15 00:10:39
│ └── Chason: 一针见血，问题精简到位[赞同] 👍🏽0 💭N/A IP 🕐2021-08-02 15:44:22

知乎用户7Xn636: 看到没，这就数学的恐怖之处。非要把猪毒死，留着吃排骨他不香么？ 👍🏽47 💭N/A IP 🕐2020-06-10 10:41:53

│ └── 穿山甲到底说了啥: 我有点能理解为什么google出题用的小白鼠了[思考] 👍🏽37 💭N/A IP 🕐2020-06-10 14:09:25
│ └── 知乎用户yPVCP6: 小白鼠发起抗议，同样是哺乳动物，凭什么狗狗就可以养尊处优[好奇] 👍🏽2 💭N/A IP 🕐2020-06-10 15:44:34
│ │ └── 霍州韩胖胖: 因为繁殖能力强大，好用，是完美的实验对象 👍🏽9 💭N/A IP 🕐2020-06-10 19:17:08
│ │ └── 尹立岩: 单身的那种吗？[思考] 👍🏽0 💭N/A IP 🕐2020-06-10 19:26:14
│ └── 令狐重阳: 小白鼠:听听这说的是人话么 👍🏽0 💭N/A IP 🕐2020-06-12 08:31:58

被芯片耽误的厨子: 你一个硕士，怎么给我的感觉就好像是博士以上的水平，这就离谱 👍🏽31 💭N/A IP 🕐2020-06-10 11:20:17

│ └── 败犬不需要安可: 或许这就是段位差距吧，好比斗尊和斗帝 👍🏽22 💭N/A IP 🕐2020-06-10 14:02:34
│ │ └── 被芯片耽误的厨子: 我也就是个大斗师 👍🏽1 💭N/A IP 🕐2020-06-10 14:42:26
│ │ └── 谁都没想到的昵称: 消炎，越级单杀 👍🏽0 💭N/A IP 🕐2021-10-20 14:37:38
│ └── 热带栗子球: 说实话，作者应该是硕士中的至强者了，作为学通信的在读小硕，太佩服作者了。 [棒] 👍🏽10 💭N/A IP 🕐2020-06-10 21:26:13
│ └── 亚尔斯兰战记: 信息论的创始人香农提出信息论的时候是在他的硕士论文里 👍🏽0 💭N/A IP 🕐2022-08-04 08:05:21

GrossteAnmassung: 没想到今晚刷到你这篇回答，真是有幸，对我有一种打开了新世界大门的感觉[害羞] 👍🏽386 💭N/A IP 🕐2020-06-10 05:05:41

知乎用户Rbu8c5: 中国足球的例子好 👍🏽22 💭N/A IP 🕐2020-06-10 09:08:26

四处游荡的风: 原来信息论是这么用的。我一直觉得这只是一个奇奇怪怪的数学理论而已。[捂脸]香农祖师爷，我错了。[捂脸] 👍🏽14 💭N/A IP 🕐2020-06-10 13:48:21

│ └── 名杨: 数字逻辑课的内容都快忘光了，就还记得老师第一节课说：作为CS专业的学生，不可以不知道香农。 👍🏽4 💭N/A IP 🕐2020-06-10 23:31:09
│ └── CPPNB: 数字逻辑。。。。我们已经开始玩器材了，好难！你咋过的，我觉着我过不了 👍🏽0 💭N/A IP 🕐2020-06-12 06:29:42
│ └── 名杨: 全靠老师放水~~~ 👍🏽1 💭N/A IP 🕐2020-06-12 07:09:25
│ └── May: 你们老师这么实在慧眼识60 👍🏽0 💭N/A IP 🕐2020-09-26 13:58:20

捶呀捶: 作者您好，文中这一部分，猪喝完水以后都用两种状态，生或者死，因此信息熵为H=-(0.5log0.5+0.5log0.5)，这一部分，我不太理解。猪喝完水以后确实有两个状态，但这两个状态发生的概率何为都是0.5呢？如果题目加上这这样一个条件，“喝了有毒的水的猪，有50%的概率会死”的话，这一部分的信息熵有应该如何算呢？ 👍🏽16 💭N/A IP 🕐2020-11-19 11:40:12

│ └── 拉普拉斯变形金刚: 同问[赞同] 👍🏽0 💭N/A IP 🕐2022-01-05 15:42:42
│ └── 周zzzzzyq: 把所有的水对半分成两份肯定有一份有毒一份没毒 👍🏽0 💭N/A IP 🕐2022-01-18 23:27:47

信息安全从业者: 太强了，强的不是最后的进制转换，是之前将问题用信息论的方式去解决的思想，有种高屋建瓴的感觉。 👍🏽12 💭N/A IP 🕐2020-06-10 17:32:05

│ └── 薛康泰: 如果1000桶水里有10桶有毒，又该怎么算呢 👍🏽0 💭N/A IP 🕐2023-09-01 11:16:37

董四火: 牛批虽然公式看不懂得去补数学了 👍🏽7 💭N/A IP 🕐2020-06-10 12:00:02

│ └── 一块黑夜: 哈哈哈，补数学没用哦 👍🏽1 💭N/A IP 🕐2020-06-12 03:03:53
│ └── CPPNB: 鲨仁还要猪心？ 👍🏽4 💭N/A IP 🕐2020-06-12 06:28:12
│ └── 董四火: 那就补完数学学信息论 👍🏽0 💭N/A IP 🕐2020-06-12 10:13:58
│ └── 默道人: 那就补不完了，信息论是真的很…[捂脸][捂脸] 👍🏽0 💭N/A IP 🕐2020-06-12 10:40:05

托洛茨卡娅: 你关于信息论在这里的演示非常漂亮和完备，基本回答了整个问题。但你额外补充的关于闭关锁国的论述似乎并不完备。闭关锁国的闭并非“遮天蔽日”的“蔽”，不可能阻挡太阳的能量交换，或者地球对宇宙的辐射能量，达不成热力学中所谓的“封闭系统”。清朝的统治者实际上熟知不少技术，会使用多种外语。对知识的垄断和控制才更有可能是真正的原因，也就是所谓的“弃智绝圣”。这种愚民政策，相信你很快就会发现，和国家到底是封锁还是开放或许没有很大联系。 👍🏽6 💭N/A IP 🕐2020-06-10 18:54:52

│ └── 张可枫: 这种拓展熵的思维，其实也在说智力，知识，经验，科学，的熵增吧，即信息交换过少，导致熵增，这真的很有思想启发。就像人际关系一样，善于交际的人，信息交换的更多，往往更占优势。即交换有效信息的过程，是一个熵减的过程，也就是往更有序的方向发展。 👍🏽0 💭N/A IP 🕐2023-08-20 14:57:00

宋一喵: H(X)里面两个P(x_i)是一样的吗，为什么一千桶水里面一桶有毒是-log_2(1/1000) 👍🏽6 💭N/A IP 🕐2020-06-10 12:55:32

│ └── 星夜: 因为前面还有一个求和符号，一桶水有毒的信息熵是你说的这个，但是前面还要*1/1000。 1000桶水累加1000次，正好是1 👍🏽10 💭N/A IP 🕐2020-06-12 17:54:18
│ └── 宋一喵: 感谢！ 👍🏽1 💭N/A IP 🕐2020-06-12 17:59:46
│ └── Tenn: 不好意思想再请教一下，“一枚硬币是正面”这个事件的信息熵为什么不是1/2log2(1/2)而要累加两次呢 👍🏽0 💭N/A IP 🕐2020-08-06 11:42:29
│ └── 星夜: 我觉得你过于纠结“是正面”这件事了，熵值是针对随机变量X在定义的，这里的X是硬币出现的可能性，且熵是用来描述混乱程度的，而"一个硬币是正面"这个东西是个很确定的值。你说的累加两次并不是累加，是正面的情况 + 反面的情况，结果是抛一枚硬币的结果的混乱程度。 👍🏽0 💭N/A IP 🕐2020-08-06 11:58:26
│ └── Tenn: 谢谢指正，那我这么理解可以吗：硬币的话随机事件就是“硬币的状态”，它的值域是“正面”和“反面”；水有毒的话随机事件就是“1000桶水其中有1桶有毒的状态下这1000桶水的状态”，值域是“第一桶水有毒”一直到“第1000桶水有毒” 👍🏽0 💭N/A IP 🕐2020-08-06 12:12:10

兔葵燕麦: 可其他人的答案是5啊？ 👍🏽5 💭N/A IP 🕐2020-06-10 12:56:59

│ └── 哈勃: 把答案看完，老哥 👍🏽9 💭N/A IP 🕐2020-06-10 15:54:28

虚心好学的土拨鼠: 感觉我的信息论白学了。。。哦，原来我没学过，那没事了 👍🏽4 💭N/A IP 🕐2020-06-10 13:59:15

李二狗: 看到这个答案后我只想说，“大佬，看到这两块钱了吗，现在是你的了[赞同]” 。 👍🏽4 💭N/A IP 🕐2020-06-10 13:47:15

沙漠晒女友: 以后骂人是不是可以说你话里熵量太大？ 👍🏽4 💭N/A IP 🕐2021-12-03 13:29:52

│ └── 一路向阳: X：“你的话熵更大”[飙泪笑] 👍🏽0 💭N/A IP 🕐2021-12-29 17:39:46

我呼吸了: 抬杠开始：在抛开现实只谈概念的情况下，在保证一小时内一头猪每次喝水能有结果，一小时内一头猪能喝四次水，0分钟，15分钟，30分钟和四40分钟这四个节点。那么每次需要喝250桶，而这头猪必死，因为他把所有水都喝了。因为有四个节点，那么在这四个节点中必定会在一个节点中，猪了喝水，15分钟后死了。随机扩大猪测试队列,且保证每次测试数量不变。为了方便计算设定为5。一头猪喝200桶，第一波试验，死亡一头猪。缩小有毒概率为1/200。替补猪上场，测试200桶水，每头猪喝40桶，一头猪死亡。缩小有概率为1/40。替补猪上场，测试40桶水，每头猪喝8桶，一头猪死亡。缩小概率为1/8。替补猪上场4头，每只猪1桶水，。一头猪死亡。确定有毒的水桶。一共用了11头猪，死亡4头。比答主多用一头，抬杠失败。对不起我是个菜比。 👍🏽3 💭N/A IP 🕐2021-07-30 11:40:26

│ └── 爱吃瓜的熊宝宝: 大哥你多用了6头。15分钟一次的这个只要5头猪 👍🏽2 💭N/A IP 🕐2021-08-03 12:12:19

六角盾牌: 有一个问题不是很理解，小猪死没死的信息量是1，但是为什么小猪喝了水以后死或者不死是等概率的呢？如果无毒的水更多的话，应该是小猪不死的概率更高呀。 👍🏽2 💭N/A IP 🕐2020-06-10 12:38:10

│ └── 踉跄行: 不要用概率理解。用状态理解会更好懂。 👍🏽0 💭N/A IP 🕐2020-06-10 13:44:14
│ └── 踉跄行: 只有混乱度更高（状态数量更多）的方案才能覆盖混乱度低的方案。最优的解决方案正是各状态等概率的方案。 👍🏽2 💭N/A IP 🕐2020-06-10 13:47:17
│ └── 梅诗金的实在界: 等概率分布是信息熵最大的状态，既然是是理论确定一个极限最小值，那考虑信息熵最大的情况即可 👍🏽0 💭N/A IP 🕐2020-06-10 14:39:20
│ └── 梅诗金的实在界: 其他组合情况提供的信息量如1/4 3/4只会比1/2 1/2提供的信息量小 👍🏽0 💭N/A IP 🕐2020-06-10 14:40:14
│ └── 门口问: 首先，每头猪都喝了约2^9桶水，所以概率是一样的，唯独第十头不是。其次，没必要算概率的场合，为什么要引入概率 👍🏽0 💭N/A IP 🕐2020-06-12 02:34:50

勃all in: 山东卷最后一道多选 👍🏽2 💭N/A IP 🕐2020-07-20 11:21:21

LvSatori: 这才是知乎应有的回答，看完真爽 👍🏽1 💭N/A IP 🕐2021-12-03 18:30:11

修改一下啊: shannon果然是人才。这句话信息为零[doge] 👍🏽1 💭N/A IP 🕐2021-10-22 21:17:03

知乎用户5vS2V2: 信息论是真的牛比 👍🏽28 💭N/A IP 🕐2020-06-10 08:33:26

闫雨煌: 从信息论角度越过具体实现，直接给出标准答案，确实是一个非常惊艳的思路 👍🏽1 💭N/A IP 🕐2021-08-15 02:13:40

诶呀妈呀: 为什么一个二分查找能扯这么长[飙泪笑] 👍🏽1 💭N/A IP 🕐2024-01-16 00:43:24

│ └── 你猜: 还望不吝赐教，二分法具体方案是怎么做的呀，或者在此问题下面有具体的回答吗 👍🏽0 💭N/A IP 🕐2024-12-12 17:44:33

猫线: 初中数学，四头猪就好，除去中间你给他们倒水等 👍🏽1 💭N/A IP 🕐2024-03-09 17:52:43

│ └── 猫线: 把谁桶一直分成三份，基本全都是平均分多出来的一个随便给哪一个加就好了，然后每次都是分三分， 👍🏽1 💭N/A IP 🕐2024-03-09 17:57:19
│ └── 卢笑然: 你完全没看懂 👍🏽0 💭N/A IP 🕐2025-05-16 08:19:26

知乎用户omcuyB: 让猪找个电子厂给上班的人做肉排吧 👍🏽1 💭N/A IP 🕐2022-01-17 22:40:23

龙栖息的要塞: 这是吴军老师的信息论课程里所解析的内容。 👍🏽1 💭N/A IP 🕐2021-10-29 09:11:20

一个粉刷匠: 感觉前面都讲的很好，但是熵在社会学的应用就有点扯了。按照作者的说法，如果地球上的国家都从封闭转向开放，每个国家都会“熵减”，整个地球的熵也应该减少，但地球作为一个孤立的整体，在没有外界的作用下会“熵增”，两个结果矛盾。我想说的是，自然科学就是自然科学，社会科学就是社会科学，把两个不相关领域的概念硬套可能能帮助理解，但解释力不强。 👍🏽1 💭N/A IP 🕐2025-05-09 21:19:37

电你到高: 请问十五分钟是精确的嘛？如果是精确的，可以每隔2秒钟给猪喝水，记录时间。如果刚好15分钟厚死了，那么这个组合的水就是有毒的 👍🏽19 💭N/A IP 🕐2020-06-10 10:27:34

│ └── 速速蘑菇: 信息论的结论是极限值，你这个是术的层面提问，好好看看文章在提问 👍🏽4 💭N/A IP 🕐2020-06-10 10:41:10
│ │ └── HAI Hi: 你讨论的是极限值，大部分开发是实际工作，而且实验环境和实施差别很大，既然你是实验环境，那更应该明确定义。 👍🏽0 💭N/A IP 🕐2021-07-26 09:16:30
│ └── 苗华栋: 题目中写有限制条件， ”1.一滴毒水足以导致一头猪的死亡。死亡时间为15分钟内不确定的某个时间点。“。不过你的思路倒是很清奇~ 👍🏽45 💭N/A IP 🕐2020-06-10 11:43:30
│ │ └── 明明就是我: 这层主的思路确实有点意思，如果真按层主这般设定，15分钟后（精确到毫秒）必死，那确实可以用一头猪在一小时内测出有毒的水。那么问题来了，这种设定下H（X）的值怎么计算呢？感觉H（X）只有等于0，才能用一头猪完成测试。不过想不明白为啥1000桶水里有一桶有毒的信息熵会是0 👍🏽1 💭N/A IP 🕐2020-06-11 23:51:14
│ │ │ └── cpu02: 我觉得可能不是H（X）变化了，可能是猪的状态增加了，猪从仅仅能有5种状态变成了剩下45分内每一毫秒都有一种状态（即在15分死的猪，在15分1毫秒死的猪，在15分2毫秒死的猪……），这个信息量实在太大了。。。按照信息论算法，这个值应该远远超过了10。。。 👍🏽4 💭N/A IP 🕐2020-06-16 22:37:55
│ │ │ └── 明明就是我: 感谢解惑，茅塞顿开。 👍🏽0 💭N/A IP 🕐2020-06-17 10:09:51
│ │ └── 鲁泽洋: 一千桶分十份，一滴都可以让🐷死亡，就把一百桶每桶取出来一点凑一桶，让🐷喝，不死下一批，死了就接着分十份，每十桶凑一桶，这样是不是能省两头猪炖排骨呢[思考] 👍🏽1 💭N/A IP 🕐2021-08-01 10:16:28
│ │ └── Koritail: 假如你是说第一个问题，那么是只能测试一次的，因为一共15分钟。假如是那个五头猪的问题，因为一共能测试4次，你这种方法反倒在后面测试中因为猪死了而不能继续测试所以需要的猪反而更多 👍🏽0 💭N/A IP 🕐2022-01-15 17:18:17
│ └── Loki: 新的问题1000桶水如何做到两秒喂一口[为难] 👍🏽6 💭N/A IP 🕐2020-06-10 14:14:50
│ │ └── 菠菜豆腐: 这个可以有，实验准备充分就行，比如水倒在烧杯里，控制好猪，用滴管喂，一组人喂一组人换烧杯一组人计时。 👍🏽0 💭N/A IP 🕐2020-06-12 06:17:01
│ │ │ └── May: 成本也挺高的 👍🏽0 💭N/A IP 🕐2020-09-26 13:50:58
│ │ └── 咿呀咿呀: 就不能用一千头猪一起来 👍🏽0 💭N/A IP 🕐2021-08-05 16:49:10
│ │ └── 泡泡糖: 能是能，单用数学0成本省下来995头猪，拿来炖排骨不香么。 👍🏽0 💭N/A IP 🕐2021-10-25 11:23:01
│ │ └── 咿呀咿呀: 主要是省下来了不一定是自己的 👍🏽0 💭N/A IP 🕐2021-11-09 21:24:31
│ └── 知乎用户nonL4d: 猪的死亡时间在15分钟内是不确定的 👍🏽0 💭N/A IP 🕐2020-06-10 16:47:22
│ └── 饱死荷兰豆: 就是你这个是工程问题，他说的是理论问题 👍🏽0 💭N/A IP 🕐2020-06-10 21:32:22
│ └── 西朝午: 感觉你没理解这个东西，这么说吧，第一头猪在第零秒就喝下了199桶里的水 👍🏽0 💭N/A IP 🕐2020-06-11 22:50:29
│ │ └── 西朝午: 呸呸呸，两百桶 👍🏽0 💭N/A IP 🕐2020-06-11 22:54:39
│ └── 白毛小狼狗: 你这个理解跟我第一反应一样。 👍🏽0 💭N/A IP 🕐2021-05-27 15:09:05

OGRE: 一点提议，或许负熵的说法在生命科学中还有一定价值，但个人觉得把熵的概念推广到社会科学略显牵强，比如全球各国加在一起基本算是个孤立体系，那岂不是全球政治经济体系必将导向混沌和无序？另一方面，如果一个国家对外扩大交流，学习先进经验是引入负熵，等价于向外转移熵，那这就是不再是一个双赢过程，而是损人利己，而且考虑到熵稳定律，损人的程度还比利已更高，这显然与全球化合作共赢的理念相悖，倒是和懂王有些不谋而合[捂脸] 👍🏽14 💭N/A IP 🕐2020-06-11 16:19:55

│ └── 饭团: 所以有周期论啊，几百年一轮回 👍🏽0 💭N/A IP 🕐2021-06-14 09:41:20

晕晕的坦克: すごい！！！这就学信息论。[超开心] 👍🏽10 💭N/A IP 🕐2020-06-10 09:36:35

知乎用户MhxrON: 就是新世界的大门被打开了 👍🏽9 💭N/A IP 🕐2020-06-10 10:18:25

Hirogyo: 您好，我有一个问题。因为喝第一桶水时，喝到毒水的概率是千分之一，也就是死亡的概率是1/1000，猪每喝一桶水「活着」和「死亡」两个事件概率并不是均等的。但计算「一只猪喝完水后的状态」的信息熵时直接用1/2 就行吗？ 👍🏽8 💭N/A IP 🕐2020-06-10 14:55:51

│ └── Gooooooo: 其实正确的说法应该是，在没看到这一头猪的时候，生死概率各是1/2，与它喝水没有无关。就当作一个不能观察的黑屋子，里面有水，把编号1～n的猪送进去，它们以预设的最高效率的方法去试毒，15分钟后打开屋子看活着哪些，就能推测出哪桶有毒。如果n小于5肯定全死了。在没开屋子之前猪活着概率就是1/2 👍🏽0 💭N/A IP 🕐2021-12-16 00:42:13
│ └── 西瓜小奶糖: 薛定谔的猪了属于是[飙泪笑] 👍🏽0 💭N/A IP 🕐2021-12-24 02:23:23

light moon: 小白不懂就问：“如果至少需要n头猪能够找到这桶毒水，那么随机变量Y的信息熵必须要大于随机变量X的信息熵”这个是为什么？ 👍🏽5 💭N/A IP 🕐2020-06-10 09:25:43

│ └── 杨通卓: 通俗的讲，只能通过信息量大的事情推出信息量少的事情，比如说能通过“张三是北京人”推出“张三是中国人”，因为北京人的信息量比中国人更大；反过来不行。 👍🏽53 💭N/A IP 🕐2020-06-10 09:55:51
│ │ └── light moon: [思考]，H为信息熵，信息熵降低需要外界提供信息量，即理论上信息熵小的一边它的信息量是要比信息熵大的一边大的呀，还是没太明白的亚子…… 👍🏽5 💭N/A IP 🕐2020-06-10 10:00:29
│ │ │ └── light moon: 又想了一下，外行的一点通俗理解：可以用混乱度大的来检测小的➡️信息熵大的只要给它信息就可以减小信息熵，反过来却没法在不增加别的条件情况下让一个信息熵小的事物变大——这涉及信息的不可逆，有个理论叫“知识的诅咒”，即一个信息你知道了就再也没法回到不知道的状态了。所以只能用信息熵大的事物来检测信息熵小的事物（信息熵大的事物可以包含信息熵小的事物的所有信息）[思考] 👍🏽4 💭N/A IP 🕐2020-06-10 11:17:18
│ │ │ └── AllGone: X：1000桶里有一桶为毒水；Y：n只猪喝完水后的状态；我们的目标是：确定n的值，即使Y的信息量增加，取到Y的最小信息熵。通过X的信息熵9.966能推导出的Y的最小信息熵即为10。 👍🏽1 💭N/A IP 🕐2020-06-10 11:20:29
│ │ │ │ └── 柳飞扬: 底数是2可以这样，但是比2小呢？ 👍🏽0 💭N/A IP 🕐2021-02-22 10:29:13
│ │ │ └── 崔亚杰: 感觉信息量是个变化值，表示的是两个信息熵的差值，如果参考对象不同的话，比较两个变化值是不科学的，不知道理解的对不对。 👍🏽0 💭N/A IP 🕐2020-06-10 12:06:40
│ │ └── 饱死荷兰豆: 类似于不等式里的小范围推出大范围 👍🏽0 💭N/A IP 🕐2020-06-10 21:31:37
│ │ └── F发发发: 你这个例子举的俩个信息量的核心是张三，这才能根据信息量大推信息量小的吧，一千桶水和猪喝水后状态，这俩能比较嘛？ 👍🏽0 💭N/A IP 🕐2020-06-11 08:53:11
│ │ └── Ringzl: 二者是一个问题，不用拆开，猪喝水后的状态确定了，哪桶水有问题肯定确定了。二者等价的。 👍🏽0 💭N/A IP 🕐2020-06-11 11:10:51
│ └── 苗华栋: n头猪的信息熵可以理解为这n头猪信息的不确定度。也可以这样理解信息熵，这n头猪需要确定一个信息时，如果将信息完全确定下来，也就是让熵降为0，所能提供最大的信息量就是2.3219n（正文里提到信息熵和信息量的区别），我们也可以把它想象成带宽，或者信道容量。一个带宽是2.3219n的通道，不可能承载信息熵更大的信息，就好比带宽是100Mbps，下载速度一定在带宽以下，不可能达到千兆光纤的效果。 👍🏽13 💭N/A IP 🕐2020-06-10 12:03:46
│ │ └── light moon: 感谢回复！ 👍🏽0 💭N/A IP 🕐2020-06-10 12:09:48
│ └── 潇洒的一把梭: 简单理解：Y的总状态数组成的状态空间大于X的状态空间，你就能找到一个Y到X的满射来得到答案。 👍🏽6 💭N/A IP 🕐2020-06-10 12:34:40
│ │ └── 十六号样本: 理解了，要做的事情原来有两件。第一件确定最小的猪的数量使得Y状态空间大于X状态空间；第二件事是构建Y到X的满射。感谢赐教。 👍🏽4 💭N/A IP 🕐2020-06-12 17:25:56
│ │ └── 潇洒的一把梭: yeah 👍🏽0 💭N/A IP 🕐2020-06-12 18:31:50
│ └── Ringzl: 我的理解是随机变量Y的信息熵表示的是n只猪状态(在四个时间段内挂或存活)的不确定性。随机变量X的信息熵表示的是事件(1000桶有一桶毒水)的不确定性。目标是要确定X，就是将X的熵减为零，让事件确定下来。不确定性越高，信息量越大(可能性越多)，当H(Y)>H(X)，在事件Y确定的条件下，一定能确定事件X。 👍🏽2 💭N/A IP 🕐2020-06-10 22:35:13
│ │ └── 恒今: 明白了明白了[大笑]，谢谢 👍🏽0 💭N/A IP 🕐2020-06-11 17:21:45
│ └── 傻白前辈: n是外部输入信息，当n能使信息熵H(Y)降为0时，说明n的信息量够大，比H(Y)更小的信息熵H(X)一定可以被n降为0。 👍🏽2 💭N/A IP 🕐2020-06-11 16:35:09
│ └── Tonychanlucky2020: 有个问题，答案是5头，所以Y是小于X 👍🏽0 💭N/A IP 🕐2021-12-07 09:28:10

胜勋: 死猪可以喝水吗？第一次死掉了，这只猪还能否继续做第二次实验？ 👍🏽30 💭N/A IP 🕐2020-06-10 07:41:54

│ └── 枫叶童话: 死掉了你不就知道哪桶有毒了 👍🏽290 💭N/A IP 🕐2020-06-10 08:07:19
│ │ └── 随心所欲: 有时间限制 👍🏽0 💭N/A IP 🕐2020-08-12 10:47:55
│ └── 左拉: 没认真听讲，下课来办公室[捂嘴] 👍🏽192 💭N/A IP 🕐2020-06-10 10:27:12
│ └── 知乎用户G3xuD6: 这套题的本质是用10位二进制数表示1到1000的任意数字。 👍🏽31 💭N/A IP 🕐2020-06-10 13:36:55
│ │ └── 水木杉: 数学白痴的我，看到这句话才似懂了~~ 👍🏽0 💭N/A IP 🕐2020-06-12 12:30:01
│ │ └── Astrid: 好像是五位五进制数表示吧。每一位有五个状态。 👍🏽0 💭N/A IP 🕐2020-06-13 07:31:38
│ └── 郝健民: 死猪可以喝水那就不止5种状态了 👍🏽28 💭N/A IP 🕐2020-06-10 13:57:12
│ └── Loki: 死猪可以喝水，但无法再死了[看看你] 👍🏽31 💭N/A IP 🕐2020-06-10 14:12:40
│ │ └── BUG: 你他娘的真是个小机灵鬼[捂脸] 👍🏽0 💭N/A IP 🕐2021-05-29 22:36:06
│ └── Cris.cheng: 用某一只猪死的时间来判断该位的值，死掉了那个位置的值就得到了。 👍🏽3 💭N/A IP 🕐2020-06-10 15:05:06
│ └── 老三: 如果五头猪都是第一次喝就死了，十五分钟就知道那个有毒了 👍🏽3 💭N/A IP 🕐2020-06-10 16:46:38
│ └── 杨指北: 没想到这竟然能有11个赞…… 👍🏽7 💭N/A IP 🕐2020-06-10 17:20:52
│ │ └── 一块黑夜: 因为他们没耐心看下去呗 👍🏽0 💭N/A IP 🕐2020-06-12 02:59:59
│ └── 兔兔真好吃: 如果水喝完以前猪就死了，但总量是不变的，编码仍然有效，只需要手工补齐后边的数位就可以了。 👍🏽1 💭N/A IP 🕐2020-06-10 18:27:04
│ └── 韭菜邦邦硬: 本末倒置了，目的是找出哪桶水有毒，喝水只是手段… 👍🏽3 💭N/A IP 🕐2020-06-10 19:09:01
│ └── 尹立岩: 死猪可以喝水，可以再死，那就是15种状态了，3头猪就够用了 👍🏽1 💭N/A IP 🕐2020-06-10 19:21:38
│ │ └── 蔺笑天: 为什么不是16种不是2^4么 👍🏽0 💭N/A IP 🕐2020-06-10 22:08:55
│ │ └── 尹立岩: [捂脸]我算错了 👍🏽0 💭N/A IP 🕐2020-06-10 23:35:46
│ └── 你若很有涵养: 要保证它的死是有意义的 👍🏽1 💭N/A IP 🕐2020-06-10 20:33:30
│ └── 田子何: 能，检验一下死亡是否是吸收态。即便是真理也得反复接受实践检验。万一喝复活了，那信息量不是一般的大 👍🏽3 💭N/A IP 🕐2020-06-10 20:48:27
│ └── 互联网海贼: 只有一杯水有毒，所以编码只有一个那杯水编码是一定的，在某一位上是固定的不会有两个值，所以某时刻猪死了，那个位就定了，不用再改了，所以死猪也不用再喝了 👍🏽1 💭N/A IP 🕐2020-06-10 21:33:55
│ └── 西木: 算权重啊 👍🏽0 💭N/A IP 🕐2020-06-11 19:03:21
│ └── 紫梓: 这5组不是满了吗 👍🏽0 💭N/A IP 🕐2020-06-11 23:05:43
│ └── 不在读程序员: 死掉了不就得出结论了吗。 👍🏽1 💭N/A IP 🕐2020-06-12 06:29:39
│ └── 涅槃: 就是靠哪只猪死掉来确定5进制数哪个位置上的数字不是0，靠死掉的这只猪是第几次喝水死的，来确定该位置上的数是1234中的哪个，靠最终不死的猪来确定该位置上的数字是0，这样，5只猪就确定了唯一的一个5位五进制数，这个数就是毒水的序号。最大的五进制数44444相当于十进制的3124，这就是答主所说的“不仅可以检测1000桶水，甚至检测3000桶水都是没有问题的”的原因。 👍🏽2 💭N/A IP 🕐2020-06-20 16:42:09
│ └── 1428: 能不能算出4只猪来测的成功率 👍🏽1 💭N/A IP 🕐2020-07-03 16:26:48
│ └── 笑死我了: 因为只有一桶水有毒，该位以后为0了。 👍🏽0 💭N/A IP 🕐2020-08-31 13:31:03
│ └── May: 可以涮肉试试 👍🏽0 💭N/A IP 🕐2020-09-26 13:46:55
│ └── 哈哈哈嗝哈哈: 你这，第一回就抽中了还要啥自行车 👍🏽0 💭N/A IP 🕐2021-06-29 17:36:56
│ └── Impact wave: 九漏鱼？[捂脸] 👍🏽0 💭N/A IP 🕐2021-07-30 20:57:59

斯芮狄普斯: 眼前一亮 👍🏽4 💭N/A IP 🕐2020-06-10 08:09:57

风吹落花如雪: 洋洋洒洒一大篇，可惜答案完全错误，不过已经装逼了 👍🏽3 💭N/A IP 🕐2020-06-10 22:10:22

│ └── 量子态的小鼠: 你再看看？ 👍🏽1 💭N/A IP 🕐2020-06-11 00:38:30
│ └── 木已成舟: 怎么错了？ 👍🏽0 💭N/A IP 🕐2022-01-18 13:07:20

123456: 狠一点四头也是可以的[惊喜] 👍🏽3 💭N/A IP 🕐2020-06-10 13:33:56

│ └── 一块黑夜: 不可以哦，最少五只，你仔细读读看 👍🏽0 💭N/A IP 🕐2020-06-12 03:06:36
│ │ └── 123456: 看过了啊，没说毒不死人啊[好奇] 👍🏽6 💭N/A IP 🕐2020-06-12 05:33:30
│ │ └── 苍山负雪: [飙泪笑][飙泪笑][飙泪笑][飙泪笑][飙泪笑]没必要把自己搭上 👍🏽4 💭N/A IP 🕐2020-06-12 09:14:11
│ │ └── 苗华栋: 才领会到你的笑点 [哈哈] 👍🏽1 💭N/A IP 🕐2020-06-12 12:22:14
│ │ └── 七月: 请对自己好一点[大笑] 👍🏽1 💭N/A IP 🕐2020-06-16 09:29:27
│ │ └── 123456: 吃顿好的[好奇] 👍🏽1 💭N/A IP 🕐2020-06-16 10:54:12
│ └── 陈愚: 你真的是一个人才…… 👍🏽0 💭N/A IP 🕐2020-06-17 08:48:13
│ └── M.徐: 太秀了吧！ 👍🏽0 💭N/A IP 🕐2021-07-27 18:47:28

casper: 猪：我喝不了那么多水！ 👍🏽2 💭N/A IP 🕐2020-06-11 15:59:17

孩子们快跑啊: 妙啊本来决策树这一块不理解的，现在解决了[捂脸] 👍🏽2 💭N/A IP 🕐2020-06-10 15:43:10

破晓: 身为通信系的我看完泪流满面，白学了 👍🏽2 💭N/A IP 🕐2020-06-10 14:15:18

isuper: 把所有水合起来倒进一个桶里，这桶水肯定有毒 👍🏽2 💭N/A IP 🕐2020-06-10 12:52:50

│ └── 代码练习生: 哈哈哈 👍🏽0 💭N/A IP 🕐2020-06-11 17:25:20

桃毛爸爸: 第一头猪要喝500桶水，撑死了[捂嘴] 👍🏽2 💭N/A IP 🕐2020-06-10 12:43:57

│ └── 败犬不需要安可: 没必要喝完啊，和一些不就知道有没有毒 👍🏽0 💭N/A IP 🕐2020-06-10 14:03:48
│ └── 似影中仙: 一桶喝一滴 👍🏽0 💭N/A IP 🕐2020-06-10 15:51:12
│ └── 于逊: 5进制，第一头猪只需喝200滴。[思考] 👍🏽0 💭N/A IP 🕐2020-06-10 22:46:00
│ └── 名杨: 嗯？不是每头猪都要喝500桶吗？ 👍🏽0 💭N/A IP 🕐2020-06-10 23:24:12
│ │ └── 西朝午: 二进制的话，第二头猪只需要喝250桶，第三头125桶，以此类推（应该是） 👍🏽0 💭N/A IP 🕐2020-06-11 22:59:03
│ │ └── hyyy: 每头猪都要喝500桶里的一滴 👍🏽0 💭N/A IP 🕐2020-06-22 14:13:06
│ └── 门口问: 第二头也是。而且只是一勺混合了500桶水的水 👍🏽0 💭N/A IP 🕐2020-06-12 02:35:40

礼拜天: 第三次看了这个回答厉害工程上的状态映射找方案学到了想想香农在知乎神位更加离谱了[捂脸] 👍🏽2 💭N/A IP 🕐2021-05-03 18:38:24

蒋甬杭: 用信息论做过一道：12个球，其中一个质量不同，用天平秤3次找出来的题。http://blog.sina.cn/dpool/blog/s/blog_4723adba0100bm0f.html 👍🏽2 💭N/A IP 🕐2021-02-14 06:37:34

│ └── 炸弹卡车歼16: 对，我以前在一本收录各种逻辑学题目的书上看过类似的题[惊喜] 👍🏽0 💭N/A IP 🕐2021-05-27 18:52:32

心有萌虎: 答主nb，很清晰。不过在分配猪喝水时不是很清楚，相信很多人没看懂为什么要那样实现。提供一个思路以供参考。确定猪有5种状态以后，采用5进制编码。如82变为00312。这样每桶水都有一个唯一的5进制编码。其中0代表永远不给这头猪喝这个水，3代表第3轮给这头猪喝这个水。这样来实现把水分配给猪喝。然后就是和答主说的一样了，根据猪的死亡情况来确定编号。这样也可以简单的得出，5头猪一共可以检测5的5次方，即3125桶水（3125可以编码为00000，即这桶水不给任何猪喝，最后也没有猪死） 👍🏽2 💭N/A IP 🕐2020-08-01 16:45:24

雨夜无眠yn: 我想问如果是两桶有毒的话，还能用这种办法计算吗？ 👍🏽1 💭N/A IP 🕐2020-07-02 16:45:15

│ └── 苗华栋: 可以，计算方法差不多，但方案就复杂很多。 👍🏽1 💭N/A IP 🕐2020-07-02 18:02:55
│ └── Syan: 如果只知道有毒但不知道有几桶水是有毒的话，这种类似于一个小区1000个人做核酸检测的理论极限要如何计算呢 👍🏽0 💭N/A IP 🕐2021-08-01 19:26:27

Inf: 这个思路太巧妙了，我联想到无砝码天平称球的问题，例如http://www.zhihu.com/question/33250659，用相同的方法便可在不给出具体方案的前提下得到所需的最少称重次数（虽然具体的称重步骤也很简单）。 👍🏽1 💭N/A IP 🕐2020-06-19 01:11:03

为什么不准收藏: 最后的社会熵增细思极恐啊，如果全世界也是一个封闭系统，想要某个国家维持低熵状态就必然要把其他国家变得更高熵。但是当所有其他国家的熵都没办法更高时，这唯一一个低熵国也要慢慢变成高熵国了。这不是必死吗？所以感觉似乎哪里不对啊 👍🏽1 💭N/A IP 🕐2020-06-12 08:53:45

马马牛: 我是磕着瓜子点开的这个问题，然后认认真真的做了2页笔记 👍🏽1 💭N/A IP 🕐2020-06-10 21:57:34

│ └── superG: 我是事后贤者时间抽烟的时候翻到的这个问题，然后下床扒出了压箱底的教科书看了一夜 👍🏽2 💭N/A IP 🕐2021-05-30 16:25:40
│ └── 大玩子: 你就离谱[doge] 👍🏽0 💭N/A IP 🕐2021-12-07 10:59:39

会敲代码的喵: 为什么你又让我回想起大学时学习信息论的恐怖……头秃…… 👍🏽1 💭N/A IP 🕐2020-06-10 17:42:05

黑翼: 这个看似迫害猪猪的问题居然隐藏着聪明人的奥义 👍🏽1 💭N/A IP 🕐2020-06-10 17:38:36

Jeremy: 有点不懂，把国看做一个系统，闭国所以国亡。但是开放交流只是把国放成一个球，球为一个系统，所以球亡？只是时间延长到人类不用担心的值？ 👍🏽1 💭N/A IP 🕐2020-06-10 17:26:01

│ └── 冷夜: 但是球使用了球外提供的能量（太阳）啊，球和太阳看成一个系统，人类不能在系统崩溃前（基本就是太阳熄火前）利用太阳系以外资源也是必亡，看起来是不是比较合理了扩大到宇宙，不能利用宇宙外资源，必亡，这就是热寂（宇宙未来一个可能的结局） 👍🏽0 💭N/A IP 🕐2021-10-25 01:46:55
│ └── 冷夜: 当然，关于作者国家这一段完全不赞成[飙泪笑] 👍🏽0 💭N/A IP 🕐2021-10-25 02:05:52

幻为之虚: 曾经面试的时候我这么回答过，然后面试官说他听不懂，，，， 👍🏽1 💭N/A IP 🕐2020-06-10 17:20:17

zimmer: 那要是找只有一桶无毒的呢 👍🏽1 💭N/A IP 🕐2020-06-10 16:55:47

蔡徐坤: 猪：我的信息载量这么大？ 👍🏽1 💭N/A IP 🕐2020-06-10 16:16:28

AloudnameQ: 奈何自己没文化，只能评论碉堡了 👍🏽1 💭N/A IP 🕐2020-06-10 15:01:43

回不去的才是回忆: 作为一个搬砖的可以告诉你，让一只猪给我一个一个喝。 👍🏽1 💭N/A IP 🕐2020-06-10 14:46:47

皓月moonqshine: 最后一部分，社会学国家闭关锁国导致熵增，应该是国家越来越死板，越来越固化吧，题主说越来越混乱，感觉有些不对劲 👍🏽1 💭N/A IP 🕐2020-06-10 14:24:28

│ └── 神仙: 本来就是胡说 👍🏽0 💭N/A IP 🕐2020-06-10 16:49:09

天伤星: 这才是知乎应该有的答案，想起我去年学信息论时的压力了 👍🏽1 💭N/A IP 🕐2020-06-10 14:11:16

是落叶复活呀: hhhhh学到了。不过想到一个搞笑的事情，猪死了，可能不是毒死的，可能是撑死的[飙泪笑]另外，从另一个角度看（有点偏题），喝完一个可以不用等到15分钟后再喝另一个。如果确定是十五分钟，不会多也不会少。或者说相差的时间很少，那么可以让间隔1分钟，或者其他间隔时间，来测试，以达到更快的速度。这个就要引入另一个变量。不过总归应该是一样的理论。 👍🏽1 💭N/A IP 🕐2020-06-10 14:08:45

│ └── 是落叶复活呀: 我看到了，是15分钟内死亡[可怜] 👍🏽0 💭N/A IP 🕐2020-06-10 14:11:03
│ └── 美个: 哈哈哈撑死 👍🏽0 💭N/A IP 🕐2020-06-11 22:28:33
│ └── 一块黑夜: 那你也应该看到人家说这是理想型猪，撑不起 👍🏽0 💭N/A IP 🕐2020-06-12 03:08:27
│ └── 美个: 我只是笑她说的搞笑而已 👍🏽0 💭N/A IP 🕐2020-06-12 10:02:50

树洞: 为什么要把简单的问题复杂化呢？ 👍🏽1 💭N/A IP 🕐2020-06-10 14:06:18

│ └── wing: 是啊，一个简单的进制问题，小学生说一遍都能听懂。。。 👍🏽2 💭N/A IP 🕐2020-06-10 14:13:56
│ └── 四处游荡的风: 这应该是把简单的问题规范化。 👍🏽1 💭N/A IP 🕐2020-06-10 16:01:35
│ └── 昨天周六: 因为不这么做问题一复杂就做不出来了[捂脸] 👍🏽2 💭N/A IP 🕐2020-06-10 19:32:37
│ └── 10号: 把简单的问题复杂化是为了解决更复杂的问题 👍🏽8 💭N/A IP 🕐2020-06-10 21:29:49
│ └── PassiveOB: 如果是几千万桶水，更多的猪和时间，答主一样能做 👍🏽4 💭N/A IP 🕐2020-06-10 21:44:07
│ └── bicbrv: 这个其实叫把具体问题泛化（generalize） 👍🏽0 💭N/A IP 🕐2020-07-03 11:20:47

未完成: 佩服 👍🏽1 💭N/A IP 🕐2020-06-10 13:27:19

L.ZW: 猪喝不下这么多水怎么办？ 👍🏽1 💭N/A IP 🕐2020-06-10 13:01:11

十月钟声: 想听大佬用信息论分析一下天平假球问题。[害羞]1.有12个球，外形一模一样，其中一个为假球，假球质量轻于真球，天平无砝码，用途仅限于比较两堆物体的重量（即比较结果为左重右轻，左轻右重，左右同重三种结果之一）。需要用天平比较几次，才能保证找出假球。2.进阶版：将上述问题描述中“假球质量轻于真球”更改为“假球质量异于真球”。这里面使用一次天平可以带来的信息要如何分析，假球质量状态又会如何影响信息熵的求解？ 👍🏽1 💭N/A IP 🕐2020-06-10 12:30:57

│ └── 踉跄行: 第一种情况下，比较一次状态有三种，所以至少要比较3次。具体做法是把12个球三等分。 👍🏽0 💭N/A IP 🕐2020-06-10 13:43:46
│ └── 踉跄行: 第二种情况下，天平能传达的信息只有两个，假球在不在天平上。所以需要至少五次比较。 👍🏽0 💭N/A IP 🕐2020-06-10 14:10:06
│ │ └── 踉跄行: 四次，打错了 👍🏽0 💭N/A IP 🕐2020-06-10 14:12:27
│ │ └── 十月钟声: 第二种情况感觉并不总是2个状态。在第一次三等分之后可以增加一次真假球质量对比实验，目的是获知假球质量是轻于还是重于真球。（12个球的情况下，分成4，4，4之后，第一次使用结束，我们至少获得了4个真球）所以增加一次之后的信息状态就又成为3了，在27个球的情况下只需要4次（1次2信息实验+1次信息甄别实验+2次3信息实验）。但是不知道有没有更优秀的做法，在球数量非整倍数的时候会不会有特殊情况。 👍🏽0 💭N/A IP 🕐2020-06-10 14:56:34
│ │ └── 踉跄行: 嗯嗯，在球多的时候获取质量信息确实可以大幅减少比对次数。 👍🏽0 💭N/A IP 🕐2020-06-10 15:42:58
│ └── 令狐重阳: 两种情况下，天平带来的信息量是不变的。每次称球，都有3种结果。两种情况下不一样的是结果的可能性。第1种情况只需要知道i号球轻即可，共12种目标状态;第2种情况则不仅需要找出异常的i号球，还需要确定是轻还是重，共24种状态。当然这不影响理论所需次数，都是3。因为3^{2<12，24>3}3. 但是策略可能稍有不同。 👍🏽2 💭N/A IP 🕐2020-06-12 08:39:14
│ │ └── 十月钟声: 优秀，豁然开朗[赞同]本来还想着说想不出3次称重的方法，结果搜到一个交换球的做法，看来知道极限值跟找到最优法还是存在差距的[捂脸] 👍🏽1 💭N/A IP 🕐2020-06-12 11:26:40
│ │ └── 令狐重阳: 你可以去看一下决策树。决策树本质上和信息熵是一回事，但是不像信息熵只能理论分析，决策树可以用来指导构造具体方案。 👍🏽1 💭N/A IP 🕐2020-06-12 12:02:07
│ │ └── 十月钟声: 难道我学的是假的决策树？[捂脸]决策树除了做数据分类还能做方案？印象中按结果不同深入搜索的不是叫博弈树吗😂 👍🏽0 💭N/A IP 🕐2020-06-12 12:42:03
│ │ └── 令狐重阳: 计算机算法这部分名词翻译有时候不太统一，我们说的应该是同一个东西。 👍🏽0 💭N/A IP 🕐2020-06-12 12:50:47
│ └── 古月可可: 答案是3次，答案有了，接下来就是找出具体的过程。 👍🏽0 💭N/A IP 🕐2021-12-07 17:22:41

外星人投错胎: 一个小时后的五种状态是等概率的吗？ 👍🏽1 💭N/A IP 🕐2020-06-10 11:52:48

│ └── 苗华栋: 因为任意一桶水有毒的概率都相同，所以将它编码以后任何一个数字出现的概率也相同，猪的状态就对应了相应的编码，所以五种状态也是等概率的。 👍🏽2 💭N/A IP 🕐2020-06-10 12:06:40

自由之翼: 很简单，随便倒掉一桶，剩下的喝了如果中毒就说他们体质问题 👍🏽1 💭N/A IP 🕐2021-10-25 14:03:34

Mutex: 为啥有毒的信息熵是-log(1/1000)不是-1/1000log(1/1000)-999/1000log(999/1000)[思考] 👍🏽1 💭N/A IP 🕐2021-10-21 11:36:29

│ └── 一路向阳: 我觉得熵是集合的平均自信息量，即平均一个事件的不确定度量，集合中每个事件的发生的概率都是1/1000。 👍🏽0 💭N/A IP 🕐2021-12-29 17:48:27

公平小伙不请自来: 这他简单了。当然是一千头猪啦，一猪一桶 👍🏽1 💭N/A IP 🕐2021-07-25 10:17:16

北岛: 特么的大四的时候看这个题一拍脑袋，卧槽我会250头，一只猪一小时工作四次，1000除4得250。现在研一了看这个题：老板再给我说说信息熵咋算的[衰] 老板：先把昨天的实验做完再说[doge] 👍🏽1 💭N/A IP 🕐2021-05-27 15:33:36

席尔洛: 竟然看懂了一点点数学 👍🏽1 💭N/A IP 🕐2021-04-30 18:02:32

华山剑宗: 写的很好。但是关于如何对猪的ID的Encode没有讲到，看起来是按照位Mask来映射的。一个简单的生成式方法的Encoder/Filter： ID & Mask == Mask ，（&表示位与操作）[吃瓜] 👍🏽1 💭N/A IP 🕐2021-04-13 17:45:47

柴达木盆地: 是不是和海明码有相似之处啊 👍🏽1 💭N/A IP 🕐2021-03-12 21:40:46

│ └── River: 是相似的，计组学的知识，哈哈哈 👍🏽1 💭N/A IP 🕐2021-05-29 01:28:35

我想: 只有水的个数是5的5次方的时候概率才能取1/5。你这样的方法可不可以这样理解，我假设有3000多水，然后用概率为1/5来求n最小为5。显然该解也是1000水的解。感觉这样说严谨一些 👍🏽1 💭N/A IP 🕐2020-11-26 20:38:02

Zippo 庞岩: 感觉回到了很久以前的知乎 👍🏽1 💭N/A IP 🕐2020-09-30 20:01:37

森林不下雨: 原来信息论是这样的，高级 👍🏽0 💭N/A IP 🕐2020-09-27 13:00:46

BAZ: 如果第一次试猪就死了，那不就用一次就验证出毒水是拿桶了吗？ 👍🏽1 💭N/A IP 🕐2020-08-22 09:39:25

│ └── 椰铁遇见芭菲: 猪15min之后才死而且你怎么知道你试的就是那一桶那还做什么题你不知道你编号的桶哪桶里有啊所以才要在一个小时之内把全部试过一遍 👍🏽0 💭N/A IP 🕐2021-07-29 19:02:34
│ └── BAZ: 可这问的是至少不是吗 👍🏽0 💭N/A IP 🕐2021-08-04 17:39:40
│ └── 椰铁遇见芭菲: 你语言理解真顶级人家的至少从来不是没有把猪的条件给你整出来也就是说猪是未知的你假设已知去解题就跟你反证法先假设答案是错的然后再得出答案是错的一样这是个逻辑闭环 👍🏽0 💭N/A IP 🕐2021-08-04 17:46:53

大神周: 呵呵，你以为这样写我就能看懂了么？ 👍🏽28 💭N/A IP 🕐2020-06-10 13:52:31

pulse: 9头猪就够了，最后两桶水只用让剩下的最后一头猪喝其中一桶就够了 👍🏽0 💭N/A IP 🕐2025-09-09 21:57:41

卢笑然: 大佬，有一道询问n次审讯最多能区分出多少个囚犯中的魔鬼的题目，我看到了有人用组合数学的方法，想请教一下您能否使用信息论去做这道题？ 👍🏽0 💭N/A IP 🕐2025-05-16 08:15:14

│ └── 卢笑然: 问题链接：https://www.zhihu.com/question/1905564443343067076?utm_psn=1906623738646098443 👍🏽0 💭N/A IP 🕐2025-05-16 08:15:43

瑞雪: 有没有可能，还有更快的方法，让每头猪五分钟或者三分钟甚至一分钟喝一次，死掉时间往前推15分钟就得了[害羞][害羞] 👍🏽0 💭N/A IP 🕐2024-12-01 18:59:05

│ └── 卢笑然: 审题，15min内死去不是15min后死去。你无法判断到底是15分钟前的水还是12分钟前的水有问题 👍🏽0 💭N/A IP 🕐2025-05-16 08:16:27

阿西莫多: 明天来公司上班 👍🏽0 💭N/A IP 🕐2024-11-11 10:13:17

李一一: 有个问题就是，你不等15分钟怎么知道猪会不会被毒死，如果只需要5头猪的话。[捂脸]而且我不理解明明只需要毒死一头猪，为什么要依靠毒死那么多头猪来测试呢？如果稀释了对猪没影响，那稀释的作用是什么，这不是本末倒置吗？ 👍🏽0 💭N/A IP 🕐2024-09-25 18:00:13

李一一: 而且最少不是只需要一头猪吗，第一头头猪刚好喝到第一桶水就有毒死了。[捂脸] 👍🏽0 💭N/A IP 🕐2024-09-25 18:02:46

│ └── 卢笑然: 说的是确保分辨至少要五头 👍🏽0 💭N/A IP 🕐2025-05-16 08:17:16

空空如也: 间隔15分钟，1小时不是刚好4种状态吗 👍🏽0 💭N/A IP 🕐2024-09-17 11:10:20

│ └── 卢笑然: 五种，分别是在四个时间点死去和最后也没死 👍🏽0 💭N/A IP 🕐2025-05-16 08:17:44

当爱已成往事: [吃瓜]这理论可以用来指导油井堵水 👍🏽0 💭N/A IP 🕐2024-08-12 15:19:18

清颜: 你似乎在骂人恶作剧 👍🏽0 💭N/A IP 🕐2024-05-30 02:47:53

祝思聪: 发现计算的过程其实用了换底公式，所以如果有x头猪，每头猪结束时有n种状态，直接求[log(n)x]就行了，本质上是n进制去表示x个值最少需要几位 👍🏽0 💭N/A IP 🕐2024-01-24 13:14:48

佳佳子淦: 答主我想问下如果猪喝了毒水有1%的概率不死，这种情况怎么计算呢[流泪] 👍🏽0 💭N/A IP 🕐2023-10-25 11:54:11

拿铁女孩: 我有一个大胆的想法如果把这桶有毒的水和其他无毒的水稀释成1000桶毒性浓度千分之一的水喂给猪猪就都不会死 👍🏽0 💭N/A IP 🕐2023-10-08 13:54:09

薛康泰: 如果1000桶水里有10桶水有毒，又怎么找出这10桶呢？ 👍🏽0 💭N/A IP 🕐2023-09-01 11:25:03

单曲循环: 为什么所有公式的b都是2？b的取值怎么确定的呢？还是说无所谓 👍🏽0 💭N/A IP 🕐2023-08-08 12:35:46

│ └── 苗华栋: 都一样，取值不同，单位不同。2的时候是bit。 👍🏽1 💭N/A IP 🕐2023-08-09 19:44:05

知乎用户YO2tId: 感谢前辈启发和总结思考模式，或者是一种思维方式，收益很大。此前，我隐隐觉得数学题都是在求得边界或者极限，确定min和max值，以大类包含，明确边界。看到这篇回答，我顺便总结并理清了这种思维，即看问题直击本质，由表面及里的方式，再通过理论判定极限，避免无用功。 👍🏽0 💭N/A IP 🕐2023-02-14 02:12:36

夜林蓝: 这无法企及的高度！有种降维打击的感觉！[捂脸] 👍🏽0 💭N/A IP 🕐2022-12-31 21:16:59

谁家玉笛暗飞声: 香农对不起[大哭][大哭] 👍🏽0 💭N/A IP 🕐2022-12-30 16:08:35

fred: 猪只有不死才能进入下一轮，就是说每轮不是独立状态，也就是说五进制前提不成立。比如第一轮猪大部分死，甚至全死了，接下来如何玩？这种情况不会出现？那就不是进制 👍🏽0 💭N/A IP 🕐2022-12-29 22:41:32

无名: 扩展一下，如果是2桶有毒呢，再扩展一下、如果不知道几桶有毒呢？怎么从数学上证明？ 👍🏽0 💭N/A IP 🕐2021-11-12 21:32:23

FlankerCT: 答主赞数和香农论文引用数相当[惊喜] 👍🏽0 💭N/A IP 🕐2021-10-28 20:03:00

蓝黑老汪: 7头 👍🏽0 💭N/A IP 🕐2021-10-27 14:29:34

光哥: 是不是讲太复杂了？严苛情况下，每15分钟才能判断一次生死，派N只猪上场，每次能够得出（N+1）中选一。记得用天平称找出殷质量不合格的产品么？派5个猪，将水分为6堆，各吃一堆（抽样），空一堆。1000-167-28-5-1，四次确定。正推，5只猪一个小时最多能测6^{4桶水，6-36-216-1296。3125怎么来的？5}5？ 👍🏽0 💭N/A IP 🕐2021-10-27 10:07:28

o0璐0o: 就这事吧，放在书本上叫“题”放在现实中，就是有人要坐牢了 👍🏽0 💭N/A IP 🕐2021-10-25 18:53:55

风林子蓝: 这解答方式，让人想到一滴水从万米高空坠落，会对人产生多大伤害。 👍🏽0 💭N/A IP 🕐2021-10-24 10:30:50

│ └── 冷夜: 那一块冰从1米落下呢？5米呢？一块石头呢？都能用常识解答还是能一个个试？这解答方式，是把一滴水从万米高空坠落做成一个公式，只针对具体的一道题可能不比直接解决方便，但是公式出来后把水替换成任何东西把万米高空替换成任意距离都能快速得出结论。不要相信这种嘲讽科学家的反智毒鸡汤了[思考] 👍🏽1 💭N/A IP 🕐2021-10-25 02:00:46
│ └── 风林子蓝: 嗯，你要确定连下雨的常识都没有的，是科学家的话。 👍🏽0 💭N/A IP 🕐2021-10-25 09:41:34

大宝: 好像有个快速核酸检测的方法就是这样子找到病人的？ 👍🏽0 💭N/A IP 🕐2021-10-23 17:07:19

97年的小奶牛: 我家养猪场几千头，随便调来1000头，15分钟看效果就行了 👍🏽0 💭N/A IP 🕐2021-10-24 07:52:49

喜欢: 排除法算出来8头，1000桶水分n组每组取一点兑一起，1h内最多可以进行4轮试毒，1000 ÷ n ÷（n-1）÷（n-2）÷（n-3）＜1得出8头[doge] 👍🏽0 💭N/A IP 🕐2021-10-23 04:32:10

│ └── 陈宇: 和你的答案一样，原题答案分析似乎有逻辑漏洞 👍🏽0 💭N/A IP 🕐2021-10-23 09:55:47
│ └── 古月可可: 没看完吧，答主的答案是5头 👍🏽0 💭N/A IP 🕐2021-12-07 17:26:09

星月: 为什么硬币的信息熵求和后是两倍的，而有毒求和后，却不是一千倍的[思考]，是我对公式理解不对吗？求解 👍🏽0 💭N/A IP 🕐2021-10-24 08:44:17

行走的Tom: 收下我的膝盖 👍🏽0 💭N/A IP 🕐2021-10-22 21:01:35

林炜哲: 每个理论都学过，▁▁▁▁▁ [思考] 👍🏽0 💭N/A IP 🕐2021-10-23 03:48:35

知乎用户rUoUTb: 我突然想到这次疫情爆发，全面核酸检测用的方法了。10人（桶）一组，重点检测有问题的组。 👍🏽0 💭N/A IP 🕐2021-10-22 16:46:58

看破就说破: 给猪和水桶编号，一千头猪，十五分钟搞定，哈哈！ 👍🏽0 💭N/A IP 🕐2021-10-21 23:12:27

Ydai: 牛 👍🏽0 💭N/A IP 🕐2021-10-21 15:50:32

DCY: 我觉得我仿佛一头🐷 👍🏽0 💭N/A IP 🕐2021-10-21 11:47:13

老鬼: 领导不看这个。你就直接告诉领导，到底要多少头猪？ 👍🏽0 💭N/A IP 🕐2021-10-22 14:50:41

法拉盛詹姆斯: 你的回答是熵减，评论区是熵增 👍🏽0 💭N/A IP 🕐2021-10-22 00:50:20

金牛座: 智商有限，看不懂。 👍🏽0 💭N/A IP 🕐2021-10-21 14:02:56

│ └── 莫亚莫斯: 这不是智商问题，是没学过。你如果上过高中应该知道对数log，上过大学应该就能基本看懂全文 👍🏽0 💭N/A IP 🕐2021-10-23 18:16:26
│ └── 冷夜: 全文能看懂，log怎么算得回忆半天[捂脸] 👍🏽0 💭N/A IP 🕐2021-10-25 02:03:31

三秋: 好玩又牛比 👍🏽0 💭N/A IP 🕐2021-10-21 13:08:55

Harry今天困了: 我是燕双鹰[思考]。 👍🏽0 💭N/A IP 🕐2021-10-20 21:00:09

麻老虎带薪拉X: 这种回答我一般先赞再看 👍🏽0 💭N/A IP 🕐2021-10-20 15:21:15

知乎用户0V0zQw: [惊喜]重新定义了孤立系统。 👍🏽0 💭N/A IP 🕐2021-10-14 19:34:06

有故事的牛牛: 我只知道一头猪一小时只能喝4桶水，那么一小时内喝完1000桶水需要250头猪。哈哈哈其他的不会 👍🏽0 💭N/A IP 🕐2021-08-25 21:58:14

0蜻蜓队长0: 我感觉我的智商遭到了暴击[捂脸] 👍🏽0 💭N/A IP 🕐2021-08-21 16:13:27

微风: 不懂数学按照分组1000水，十猪100水一猪，死一10水一猪，死一1水一猪，死一共计12猪，用时45分钟，节省时间1/4[思考]1000水，五猪200水一猪，死一40水一猪，死一8水一猪，死一余下四猪2水一猪，死一1水一猪，死一共计7猪用时75分钟，多出时间1/4由此最佳解在7-12中间为9.5，考虑到7猪在最后一轮有1猪没有利用到，且猪没有半只的情况结果可以向7靠近，为9验算1000水，九猪八猪喝111水，一猪喝112水最坏情况，112水猪死112水分八猪喝14水一猪，猪死14水分七猪喝2水一猪，猪死最后1水一猪，猪死刚刚好一小时，但是最后一轮还是出现四猪没有利用的情况……然后突然发现嘶……这个题这样是不是可以最简单快速度找到正解1000÷n÷(n-1)÷(n-2)÷(n-3)≤1n为整数即可[思考]结论是81000÷8＝125死一猪125÷7=17.85714286约等于18死一猪(有小数点均采用向上取整原则)18÷6=3死一猪3再喝死一猪这不一个小时内测完了……8猪最优解 👍🏽0 💭N/A IP 🕐2021-08-05 16:13:08

│ └── 微风: 然后，逛了一下，隔壁五进制，只用了五头猪，就在一个小时内筛选出来了[捂脸] 👍🏽0 💭N/A IP 🕐2021-08-05 16:43:55
│ └── 微风: 就离谱 👍🏽0 💭N/A IP 🕐2021-08-05 16:44:06
│ └── 古月可可: 没看完吧，这个答主的答案就是5啊 👍🏽0 💭N/A IP 🕐2021-12-07 17:27:28

勤奋的寒号鸟: 题目说最少的情况，我的想法是有前提的①没有一头猪被毒死掉，死了数字就变大了②怎么能不被毒死，额，5头猪可以测6桶水，想不明白当我没说③一个小时15分钟一次结果，也就是说4次验证结果的机会。④第一次5头猪测1000/6份水，没有喝的那一桶刚好有毒，第二次5头猪测167/6，第三次测28/6，第四次5头猪5桶水，随便测，猪死不死都结果出来了。 👍🏽0 💭N/A IP 🕐2021-08-05 19:22:56

│ └── 勤奋的寒号鸟: 如果每次都会毒死一头猪的话最少需要6头猪，第一次6头猪测7桶水，每桶水是143份组成的；第二次5头猪测6桶水，每桶水是24份水组成的，第三次4头猪测5桶水，每桶水是5份水组成的，最后一次3头猪，5桶水，额😓空出a桶水不用，1号猪测bc两桶水，2号猪测cd两桶水，3号猪测de两桶水。应该就这样吧。 👍🏽0 💭N/A IP 🕐2021-08-05 19:51:04

路人甲: 别说没用的，现场买1000瓶矿泉水，拿一包氰化钾，再给你10头猪，试一下就知道了 👍🏽0 💭N/A IP 🕐2021-08-05 00:08:37

wangssa: 为什么不把水倒了 👍🏽0 💭N/A IP 🕐2021-08-05 11:49:08

千杯风月醉: 每个字都认识，所以，再说什么呢 👍🏽0 💭N/A IP 🕐2021-08-04 21:43:02

万马齐喑: 这收藏量离谱 👍🏽0 💭N/A IP 🕐2021-08-04 23:54:48

九千七: 虽然我看不懂，但我要点赞！[认真] 👍🏽0 💭N/A IP 🕐2021-08-04 21:45:30

心态爆炸: 一脸懵逼的进来，一脸懵逼的出去 👍🏽0 💭N/A IP 🕐2021-08-04 17:31:16

周玉丰: 我在想，一只猪能在2小时内喝几桶水[思考]水桶有多大。 👍🏽0 💭N/A IP 🕐2021-08-04 12:29:13

可怕的变态: 只需要一头猪。随便给猪喝其中一桶的水，然后把猪打死，对外宣称已经找到了有毒的水。然后如果有人买到了有毒的水就告他诽谤。[doge] 👍🏽0 💭N/A IP 🕐2021-08-04 10:09:20

一条坚忍的鱼: 随机过程也很有趣 👍🏽0 💭N/A IP 🕐2021-08-04 09:18:49

荣小鸡: 我好像读了个假的硕士[doge] 👍🏽0 💭N/A IP 🕐2021-08-03 19:07:25

醉雨梦风: 把水倒了，猪渴不死。 👍🏽0 💭N/A IP 🕐2021-08-03 22:27:46

若见花: 你没规定时间，一头不就行了吗？每五分钟喝一次，死了就往前面推算时间 👍🏽0 💭N/A IP 🕐2021-08-04 10:40:16

小老弟批瘾犯了: 给一头猪喝然后把他弄死就说毒水找到了以后万一有喝到真的就说造谣 👍🏽0 💭N/A IP 🕐2021-08-03 16:49:22

小翔哥: 看完答案才发现 1不同的猪还可以喝同一桶水呢？2十五分钟原来是个最大期限而非准确的必死时刻题目还是有些误导性 👍🏽0 💭N/A IP 🕐2021-08-03 18:56:45

我要黑桃三: 好生气感觉很有用可是我看不懂[大哭] 👍🏽0 💭N/A IP 🕐2021-08-03 22:06:29

Charles Qin: 利用排列组合的方法也能解这个问题，不必想的那么复杂。 👍🏽0 💭N/A IP 🕐2021-08-03 11:42:15

iamxyld: 最敬佩学识渊博的人，尤其敬佩数学好的人，只能用四个字来形容我此时的心情，太牛逼了 👍🏽0 💭N/A IP 🕐2021-08-03 12:22:39

知乎用户L6HE7e: 点赞的人是都看懂了吗，太牛掰了[语塞] 👍🏽0 💭N/A IP 🕐2021-08-03 19:49:30

荒原: 不懂就问，买一千条小鱼分别放入这一千桶水，限定时间内死掉的小鱼不就证明了哪桶水有毒么？或者买两千条小鱼，每个桶里放2条。 👍🏽0 💭N/A IP 🕐2021-08-03 10:55:14

午女20180330: 1号猪在15分內，喝不了500桶水啊。 👍🏽0 💭N/A IP 🕐2021-08-03 13:22:32

iamxyld: 我的答案是一只，看这只猪的运气好不好了[大笑] 👍🏽0 💭N/A IP 🕐2021-08-03 12:24:11

xxxx: 这个问题，10只老鼠即可解决，因为1000最少要用10位二进制数来表示 👍🏽0 💭N/A IP 🕐2021-08-03 09:01:46

ppppy杰: 这应该是特殊情况所以才能直接得出答案，比如说有2桶或者999桶水有毒算出来的还是实际答案吗？？ 👍🏽0 💭N/A IP 🕐2021-08-03 01:13:57

做尽荒唐事: 你在说神魔[doge] 👍🏽0 💭N/A IP 🕐2021-08-02 20:28:00

浩彡永恒: 猪肉太贵，一头都不用，999只小白鼠轻松拿下[思考] 👍🏽0 💭N/A IP 🕐2021-08-03 10:37:14

清目: 如果毒性够大，就可以多桶混合。例如，1500桶水分三组，每500桶分别取1滴水混在一起喂猪，三只猪看哪只死了，直接排除1000桶水，依次缩小范围。当然，具体最优解以及相关算法我不会。比一桶一桶试好一点吧[思考] 👍🏽0 💭N/A IP 🕐2021-08-02 15:35:01

王宇: 看不懂，至少不是最差情况吗？249头一头都没喝到咋办 👍🏽0 💭N/A IP 🕐2021-08-02 19:21:07

咕罗卜: 质检员的手，只需要一头 👍🏽0 💭N/A IP 🕐2021-08-03 09:34:14

我也很难受: 有种一群博士讨论一滴水高空落下会不会砸死人的感觉。 👍🏽0 💭N/A IP 🕐2021-08-02 17:31:11

一壶愁: 妈耶，我居然看完了[捂脸] 👍🏽0 💭N/A IP 🕐2021-08-02 07:43:18

药不然: 可以用小白鼠的我想说 👍🏽0 💭N/A IP 🕐2021-08-02 14:49:14

fujiahe: 请问为什么没有在计算中没有考虑时间限制的问题如果这道题改为15分钟内判断出来那结果会不一样吗 👍🏽0 💭N/A IP 🕐2021-08-02 14:14:54

亲爱的Sal: 每个字都认识[惊喜] 👍🏽0 💭N/A IP 🕐2021-08-02 09:58:47

teddy1027: 你这是15分钟之内搞定 👍🏽0 💭N/A IP 🕐2021-08-01 23:21:01

飞的太低了: 超过15分钟了 👍🏽0 💭N/A IP 🕐2021-08-02 07:30:43

执笔丶烟雨阁: 所以N=5？ 👍🏽0 💭N/A IP 🕐2021-08-01 14:44:52

知乎用户oKHg0q: 整个地球现在也处于“闭关锁球”的状态（没发现外星人）为什么没有效率越来越底下[好奇]。（没抬杠的意思，纯好奇） 👍🏽0 💭N/A IP 🕐2021-08-01 23:31:16

一只木鱼: 按营销，不说水有毒，喝死了就说是意外情况 👍🏽0 💭N/A IP 🕐2021-08-01 14:11:55

山药二世: 水都混一起然后就都有毒了 👍🏽0 💭N/A IP 🕐2021-08-01 15:30:09

西行寺妖: 把水都倒掉，就没有猪会死了[doge] 👍🏽0 💭N/A IP 🕐2021-08-01 09:04:57

窝凿腻马: 如果有头猪对毒药产生了免疫怎么办 👍🏽0 💭N/A IP 🕐2021-08-01 16:07:34

海威: 每次把剩余的水分两份，就变成了2的N次方大于1000 👍🏽0 💭N/A IP 🕐2021-08-01 16:02:12

得羿: 你说，那些天天学这些的人，是不是比我聪明很多[思考] 👍🏽0 💭N/A IP 🕐2021-08-01 14:57:43

执笔丶烟雨阁: 喝水时间算不 👍🏽0 💭N/A IP 🕐2021-08-01 14:26:50

周周周周周大人: 额应该是250只猪吧我猜的[大笑] 👍🏽0 💭N/A IP 🕐2021-08-01 12:07:19

大恩德胜: 1头猪就行了，还需要多少头猪？首先我们会有1000桶水和一头猪和15分钟，然后猪必然会赌死，然后我们必然有999桶水可以喝。 👍🏽0 💭N/A IP 🕐2021-07-31 15:04:29

倚天無情劍: 需要一千头猪[可怜] 👍🏽0 💭N/A IP 🕐2021-07-31 11:50:55

加加多: 有没有考虑猪不是毒死的，是撑死的[思考] 👍🏽0 💭N/A IP 🕐2021-07-31 17:30:15

路人甲: 我直接裂开这么难 👍🏽0 💭N/A IP 🕐2021-07-31 13:03:50

Teng: 刚上大二表示一点也看不懂 👍🏽0 💭N/A IP 🕐2021-07-31 09:23:25

plery: 不明觉厉，佩服佩服 👍🏽0 💭N/A IP 🕐2021-07-30 16:49:46

楚门的莫比乌斯: 500，250，125，60/60/5，30，15，7/7/1，3/3/1，1/1/1。所以，最多9头，最少6头。 👍🏽0 💭N/A IP 🕐2021-07-30 21:13:47

唯彩印刷: 别欺负猪了能换个动物吗 👍🏽0 💭N/A IP 🕐2021-07-30 22:17:34

洛殇月妖梦: 是信计专业的朋友吗 👍🏽0 💭N/A IP 🕐2021-07-30 17:46:53

帖木尔之门: 体现了算命的重要性…… 👍🏽0 💭N/A IP 🕐2021-07-30 18:51:50

擦冰: 我以为是10，答案是5，谢谢数学救了5头猪猪的命 👍🏽0 💭N/A IP 🕐2021-07-30 16:58:23

我呼吸了: 你把这道题提高到了不应该到达的高度 👍🏽0 💭N/A IP 🕐2021-07-30 10:37:27

prime: 1头啊，不喝毒水又死不了 👍🏽0 💭N/A IP 🕐2021-07-30 19:33:09

焉知非福: 所以一头猪喝第一桶水之后，一分钟后在喝第二桶，如果它在第十六分钟的时候去世了，不就证明第二桶有毒吗，[思考] 👍🏽0 💭N/A IP 🕐2021-07-30 15:10:52

Joven: 我怀疑猪是喝水撑死的[惊喜] 👍🏽0 💭N/A IP 🕐2021-07-30 12:40:14

十尤: 信息论yyds 👍🏽0 💭N/A IP 🕐2021-07-30 12:43:23

你莫批跨: 大佬牛🍺 👍🏽0 💭N/A IP 🕐2021-07-30 08:55:50

椰铁遇见芭菲: 没有人问那个桶的编码是怎么来的嘛右边第一排第一列稍微学过c语音之类的或者有了解过进制都知道但是后面的怎么来的搞不懂？？ 👍🏽0 💭N/A IP 🕐2021-07-29 19:07:19

haishinimingba: 一头猪最多喝多少水会饱 👍🏽0 💭N/A IP 🕐2021-07-29 12:09:47

昔日梦想家: 1，因为至少，刚好喝就有毒 👍🏽0 💭N/A IP 🕐2021-07-29 16:49:00

xqvier: 本人非数学专业大三学生，表示这道题心算就出来了，当然方法不一样，没有可比性[大笑] 👍🏽0 💭N/A IP 🕐2021-07-29 10:36:38

xqvier: 而且你的答案是错的，正确答案是8个 👍🏽0 💭N/A IP 🕐2021-07-29 10:55:31

│ └── 向着遥远的方向: 你在说啥？合着这一堆人都算错了就你对了？ 👍🏽0 💭N/A IP 🕐2021-07-30 03:26:50
│ └── 微风: 最优解确实是8，我也算出来了，而且并不复杂……从非专业的角度出发，你可以看看我的详细过程 👍🏽0 💭N/A IP 🕐2021-08-05 16:20:31

1000桶水，其中一桶有毒，猪喝毒水后会在15分钟内死去，想用一个小时找到这桶毒水，至少需要几头猪？-苗华栋

信息熵

题目的简化版本

原题目

熵的拓展

评论区

GrossteAnmassung: 看完这个回答我只想说一句话——教练，我想学信息论！ 👍🏽1344 💭N/A IP 🕐2020-06-10 04:02:53

风笛: 每个字都认识[大哭] 👍🏽1602 💭N/A IP 🕐2020-06-10 09:03:01

GrossteAnmassung: 没想到今晚刷到你这篇回答，真是有幸，对我有一种打开了新世界大门的感觉[害羞] 👍🏽386 💭N/A IP 🕐2020-06-10 05:05:41

三千: 这才是知乎应有的答案 👍🏽159 💭N/A IP 🕐2020-06-10 11:57:35

小池塘里的啦嘎布: 太强了，学不会[捂脸] 👍🏽113 💭N/A IP 🕐2020-06-10 07:37:11

Lloyd: 不想喝猪喝过的水咋办 👍🏽102 💭N/A IP 🕐2020-06-10 08:07:45

null: 我以为是讲算法，结果讲的是信息论，太强了 👍🏽76 💭N/A IP 🕐2020-06-10 10:24:57

牛奶咖啡8023: 感觉我的信息论白学了。。。哦，压根就没好好学过[捂脸] 👍🏽62 💭N/A IP 🕐2020-06-10 08:41:48

邓尚平: 一头猪是1bit，原问题转化为表示1000个数最少需要几位bit，妙啊 👍🏽52 💭N/A IP 🕐2020-06-10 11:42:20

知乎用户7Xn636: 看到没，这就数学的恐怖之处。非要把猪毒死，留着吃排骨他不香么？ 👍🏽47 💭N/A IP 🕐2020-06-10 10:41:53

被芯片耽误的厨子: 你一个硕士，怎么给我的感觉就好像是博士以上的水平，这就离谱 👍🏽31 💭N/A IP 🕐2020-06-10 11:20:17

GrossteAnmassung: 没想到今晚刷到你这篇回答，真是有幸，对我有一种打开了新世界大门的感觉[害羞] 👍🏽386 💭N/A IP 🕐2020-06-10 05:05:41

知乎用户Rbu8c5: 中国足球的例子好 👍🏽22 💭N/A IP 🕐2020-06-10 09:08:26

四处游荡的风: 原来信息论是这么用的。我一直觉得这只是一个奇奇怪怪的数学理论而已。[捂脸]香农祖师爷，我错了。[捂脸] 👍🏽14 💭N/A IP 🕐2020-06-10 13:48:21

信息安全从业者: 太强了，强的不是最后的进制转换，是之前将问题用信息论的方式去解决的思想，有种高屋建瓴的感觉。 👍🏽12 💭N/A IP 🕐2020-06-10 17:32:05

董四火: 牛批 虽然公式看不懂 得去补数学了 👍🏽7 💭N/A IP 🕐2020-06-10 12:00:02

宋一喵: H(X)里面两个P(x_i)是一样的吗，为什么一千桶水里面一桶有毒是-log_2(1/1000) 👍🏽6 💭N/A IP 🕐2020-06-10 12:55:32

兔葵燕麦: 可其他人的答案是5啊？ 👍🏽5 💭N/A IP 🕐2020-06-10 12:56:59

虚心好学的土拨鼠: 感觉我的信息论白学了。。。哦，原来我没学过，那没事了 👍🏽4 💭N/A IP 🕐2020-06-10 13:59:15

李二狗: 看到这个答案后我只想说，“大佬，看到这两块钱了吗，现在是你的了[赞同]” 。 👍🏽4 💭N/A IP 🕐2020-06-10 13:47:15

沙漠晒女友: 以后骂人是不是可以说你话里熵量太大？ 👍🏽4 💭N/A IP 🕐2021-12-03 13:29:52

六角盾牌: 有一个问题不是很理解，小猪死没死的信息量是1，但是为什么小猪喝了水以后死或者不死是等概率的呢？如果无毒的水更多的话，应该是小猪不死的概率更高呀。 👍🏽2 💭N/A IP 🕐2020-06-10 12:38:10

勃all in: 山东卷最后一道多选 👍🏽2 💭N/A IP 🕐2020-07-20 11:21:21

LvSatori: 这才是知乎应有的回答，看完真爽 👍🏽1 💭N/A IP 🕐2021-12-03 18:30:11

修改一下啊: shannon果然是人才。这句话信息为零[doge] 👍🏽1 💭N/A IP 🕐2021-10-22 21:17:03

知乎用户5vS2V2: 信息论是真的牛比 👍🏽28 💭N/A IP 🕐2020-06-10 08:33:26

闫雨煌: 从信息论角度越过具体实现，直接给出标准答案，确实是一个非常惊艳的思路 👍🏽1 💭N/A IP 🕐2021-08-15 02:13:40

诶呀妈呀: 为什么一个二分查找能扯这么长[飙泪笑] 👍🏽1 💭N/A IP 🕐2024-01-16 00:43:24

猫线: 初中数学，四头猪就好，除去中间你给他们倒水等 👍🏽1 💭N/A IP 🕐2024-03-09 17:52:43

知乎用户omcuyB: 让猪找个电子厂给上班的人做肉排吧 👍🏽1 💭N/A IP 🕐2022-01-17 22:40:23

龙栖息的要塞: 这是吴军老师的信息论课程里所解析的内容。 👍🏽1 💭N/A IP 🕐2021-10-29 09:11:20

电你到高: 请问十五分钟是精确的嘛？如果是精确的，可以每隔2秒钟给猪喝水，记录时间。如果刚好15分钟厚死了，那么这个组合的水就是有毒的 👍🏽19 💭N/A IP 🕐2020-06-10 10:27:34

晕晕的坦克: すごい！！！这就学信息论。[超开心] 👍🏽10 💭N/A IP 🕐2020-06-10 09:36:35

知乎用户MhxrON: 就是新世界的大门被打开了 👍🏽9 💭N/A IP 🕐2020-06-10 10:18:25

light moon: 小白不懂就问：“如果至少需要n头猪能够找到这桶毒水，那么随机变量Y的信息熵必须要大于随机变量X的信息熵”这个是为什么？ 👍🏽5 💭N/A IP 🕐2020-06-10 09:25:43

胜勋: 死猪可以喝水吗？第一次死掉了，这只猪还能否继续做第二次实验？ 👍🏽30 💭N/A IP 🕐2020-06-10 07:41:54

斯芮狄普斯: 眼前一亮 👍🏽4 💭N/A IP 🕐2020-06-10 08:09:57

风吹落花如雪: 洋洋洒洒一大篇，可惜答案完全错误，不过已经装逼了 👍🏽3 💭N/A IP 🕐2020-06-10 22:10:22

123456: 狠一点四头也是可以的[惊喜] 👍🏽3 💭N/A IP 🕐2020-06-10 13:33:56

casper: 猪：我喝不了那么多水！ 👍🏽2 💭N/A IP 🕐2020-06-11 15:59:17

孩子们快跑啊: 妙啊 本来决策树这一块不理解的，现在解决了[捂脸] 👍🏽2 💭N/A IP 🕐2020-06-10 15:43:10

破晓: 身为通信系的我看完泪流满面，白学了 👍🏽2 💭N/A IP 🕐2020-06-10 14:15:18

isuper: 把所有水合起来倒进一个桶里，这桶水肯定有毒 👍🏽2 💭N/A IP 🕐2020-06-10 12:52:50

桃毛爸爸: 第一头猪要喝500桶水，撑死了[捂嘴] 👍🏽2 💭N/A IP 🕐2020-06-10 12:43:57

礼拜天: 第三次看了 这个回答厉害 工程上的状态映射找方案学到了 想想香农在知乎神位更加离谱了[捂脸] 👍🏽2 💭N/A IP 🕐2021-05-03 18:38:24

蒋甬杭: 用信息论做过一道：12个球，其中一个质量不同，用天平秤3次找出来的题。http://blog.sina.cn/dpool/blog/s/blog_4723adba0100bm0f.html 👍🏽2 💭N/A IP 🕐2021-02-14 06:37:34

雨夜无眠yn: 我想问如果是两桶有毒的话，还能用这种办法计算吗？ 👍🏽1 💭N/A IP 🕐2020-07-02 16:45:15

马马牛: 我是磕着瓜子点开的这个问题，然后认认真真的做了2页笔记 👍🏽1 💭N/A IP 🕐2020-06-10 21:57:34

会敲代码的喵: 为什么你又让我回想起大学时学习信息论的恐怖……头秃…… 👍🏽1 💭N/A IP 🕐2020-06-10 17:42:05

黑翼: 这个看似迫害猪猪的问题居然隐藏着聪明人的奥义 👍🏽1 💭N/A IP 🕐2020-06-10 17:38:36

Jeremy: 有点不懂，把国看做一个系统，闭国所以国亡。但是开放交流只是把国放成一个球，球为一个系统，所以球亡？只是时间延长到人类不用担心的值？ 👍🏽1 💭N/A IP 🕐2020-06-10 17:26:01

幻为之虚: 曾经面试的时候我这么回答过，然后面试官说他听不懂，，，， 👍🏽1 💭N/A IP 🕐2020-06-10 17:20:17

zimmer: 那要是找只有一桶无毒的呢 👍🏽1 💭N/A IP 🕐2020-06-10 16:55:47

蔡徐坤: 猪：我的信息载量这么大？ 👍🏽1 💭N/A IP 🕐2020-06-10 16:16:28

AloudnameQ: 奈何自己没文化，只能评论碉堡了 👍🏽1 💭N/A IP 🕐2020-06-10 15:01:43

回不去的才是回忆: 作为一个搬砖的可以告诉你，让一只猪给我一个一个喝。 👍🏽1 💭N/A IP 🕐2020-06-10 14:46:47

皓月moonqshine: 最后一部分， 社会学国家闭关锁国导致熵增，应该是国家越来越死板，越来越固化吧，题主说越来越混乱，感觉有些不对劲 👍🏽1 💭N/A IP 🕐2020-06-10 14:24:28

天伤星: 这才是知乎应该有的答案，想起我去年学信息论时的压力了 👍🏽1 💭N/A IP 🕐2020-06-10 14:11:16

树洞: 为什么要把简单的问题复杂化呢？ 👍🏽1 💭N/A IP 🕐2020-06-10 14:06:18

未完成: 佩服 👍🏽1 💭N/A IP 🕐2020-06-10 13:27:19

L.ZW: 猪喝不下这么多水怎么办？ 👍🏽1 💭N/A IP 🕐2020-06-10 13:01:11

外星人投错胎: 一个小时后的五种状态是等概率的吗？ 👍🏽1 💭N/A IP 🕐2020-06-10 11:52:48

自由之翼: 很简单，随便倒掉一桶，剩下的喝了如果中毒就说他们体质问题 👍🏽1 💭N/A IP 🕐2021-10-25 14:03:34

Mutex: 为啥有毒的信息熵是-log(1/1000)不是-1/1000log(1/1000)-999/1000log(999/1000)[思考] 👍🏽1 💭N/A IP 🕐2021-10-21 11:36:29

公平小伙不请自来: 这他简单了。当然是一千头猪啦，一猪一桶 👍🏽1 💭N/A IP 🕐2021-07-25 10:17:16

北岛: 特么的大四的时候看这个题一拍脑袋，卧槽我会250头，一只猪一小时工作四次，1000除4得250。现在研一了看这个题：老板再给我说说信息熵咋算的[衰] 老板：先把昨天的实验做完再说[doge] 👍🏽1 💭N/A IP 🕐2021-05-27 15:33:36

席尔洛: 竟然看懂了一点点数学 👍🏽1 💭N/A IP 🕐2021-04-30 18:02:32

华山剑宗: 写的很好。但是关于如何对猪的ID的Encode没有讲到，看起来是按照位Mask来映射的。一个简单的生成式方法的Encoder/Filter： ID & Mask == Mask ，（&表示位与操作）[吃瓜] 👍🏽1 💭N/A IP 🕐2021-04-13 17:45:47

柴达木盆地: 是不是和海明码有相似之处啊 👍🏽1 💭N/A IP 🕐2021-03-12 21:40:46

我想: 只有水的个数是5的5次方的时候概率才能取1/5。你这样的方法可不可以这样理解，我假设有3000多水，然后用概率为1/5来求n最小为5。显然该解也是1000水的解。感觉这样说严谨一些 👍🏽1 💭N/A IP 🕐2020-11-26 20:38:02

Zippo 庞岩: 感觉回到了很久以前的知乎 👍🏽1 💭N/A IP 🕐2020-09-30 20:01:37

森林不下雨: 原来信息论是这样的，高级 👍🏽0 💭N/A IP 🕐2020-09-27 13:00:46

BAZ: 如果第一次试猪就死了，那不就用一次就验证出毒水是拿桶了吗？ 👍🏽1 💭N/A IP 🕐2020-08-22 09:39:25

大神周: 呵呵，你以为这样写我就能看懂了么？ 👍🏽28 💭N/A IP 🕐2020-06-10 13:52:31

董四火: 牛批虽然公式看不懂得去补数学了 👍🏽7 💭N/A IP 🕐2020-06-10 12:00:02

孩子们快跑啊: 妙啊本来决策树这一块不理解的，现在解决了[捂脸] 👍🏽2 💭N/A IP 🕐2020-06-10 15:43:10

礼拜天: 第三次看了这个回答厉害工程上的状态映射找方案学到了想想香农在知乎神位更加离谱了[捂脸] 👍🏽2 💭N/A IP 🕐2021-05-03 18:38:24

皓月moonqshine: 最后一部分，社会学国家闭关锁国导致熵增，应该是国家越来越死板，越来越固化吧，题主说越来越混乱，感觉有些不对劲 👍🏽1 💭N/A IP 🕐2020-06-10 14:24:28

拿铁女孩: 我有一个大胆的想法如果把这桶有毒的水和其他无毒的水稀释成1000桶毒性浓度千分之一的水喂给猪猪就都不会死 👍🏽0 💭N/A IP 🕐2023-10-08 13:54:09

喜欢: 排除法算出来8头，1000桶水分n组每组取一点兑一起，1h内最多可以进行4轮试毒，1000 ÷ n ÷（n-1）÷（n-2）÷（n-3）＜1得出8头[doge] 👍🏽0 💭N/A IP 🕐2021-10-23 04:32:10